Week 7

Lecturer: Uma Maheswari, Faculty for BITS Pilani WILP

Date: 4/Sep/2021

Topics Covered

1. Query Languages
2. Relational Algebra
   1. SELECT Operation
   2. PROJECT Operation
   3. TYPE COMPATIBILITY
   4. UNION Operation
   5. INTERSECTION Operation
   6. SET DIFFERENCE Operation
   7. Some properties for UNION, INTERSECTION and SET DIFFERENCE operations
   8. CARTESIAN (Cross Product) Operation
   9. RENAME Operation
   10. JOIN Operation
   11. OUTER UNION Operation
   12. Complete Set of Relational Operations
   13. DIVISION Operation
   14. Aggregate Functions and Grouping Operation
3. Tutorial Session
4. Post Lecture Notes

Query Languages

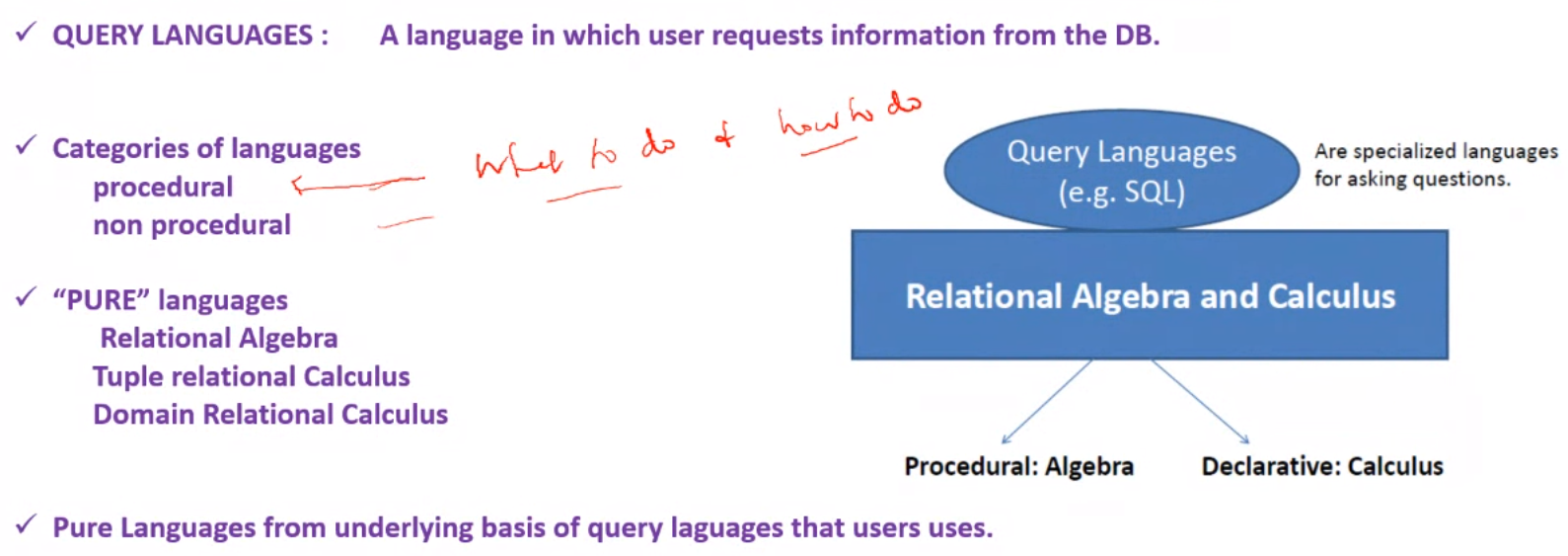
- Procedural: What to do and how to do
- Non Procedural: What to do

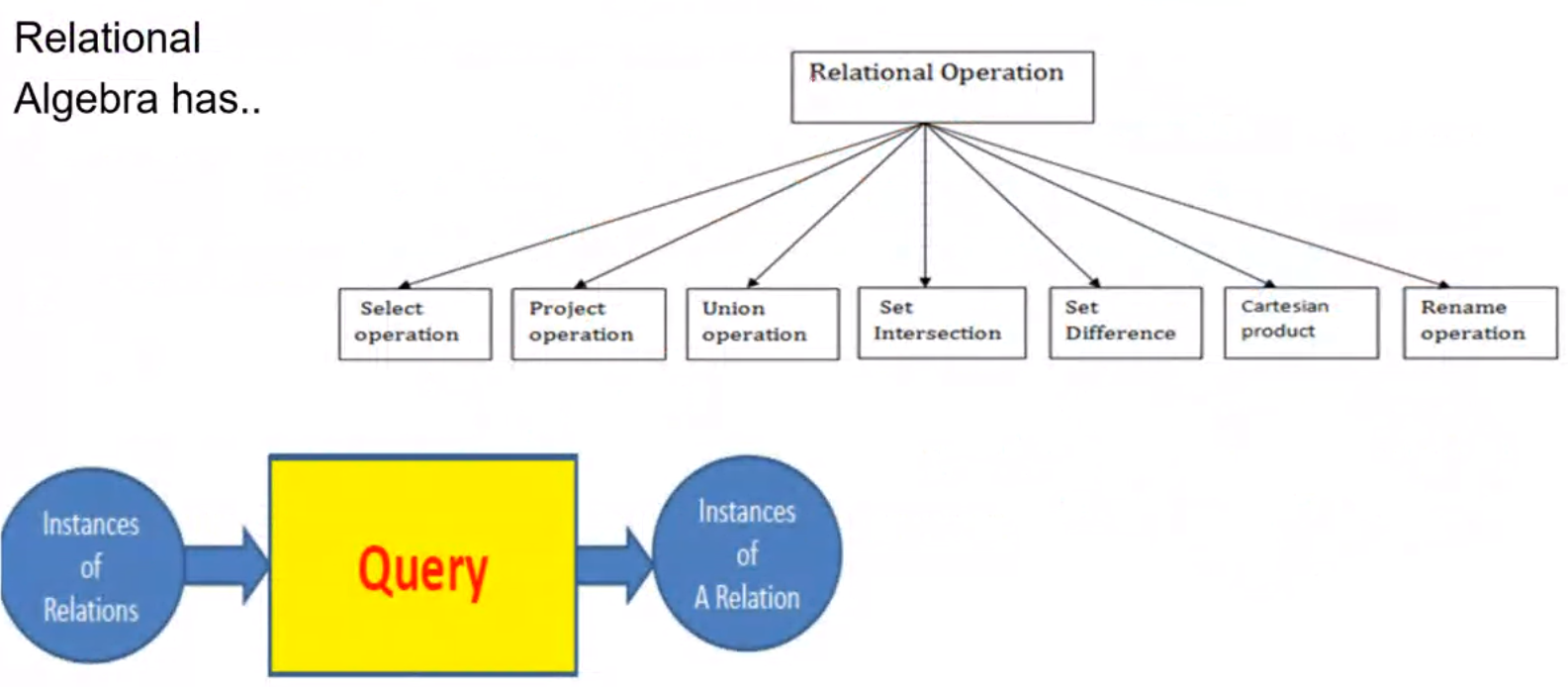
Relational Algebra

REFERENCE LECTURE

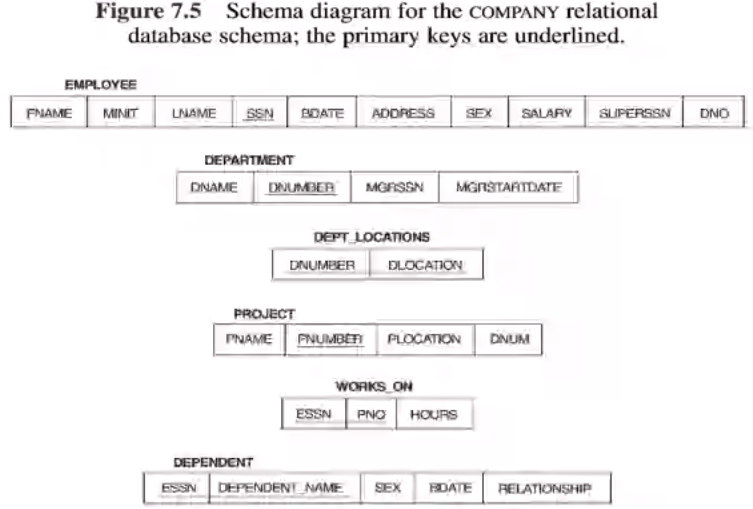
Consider the example schema

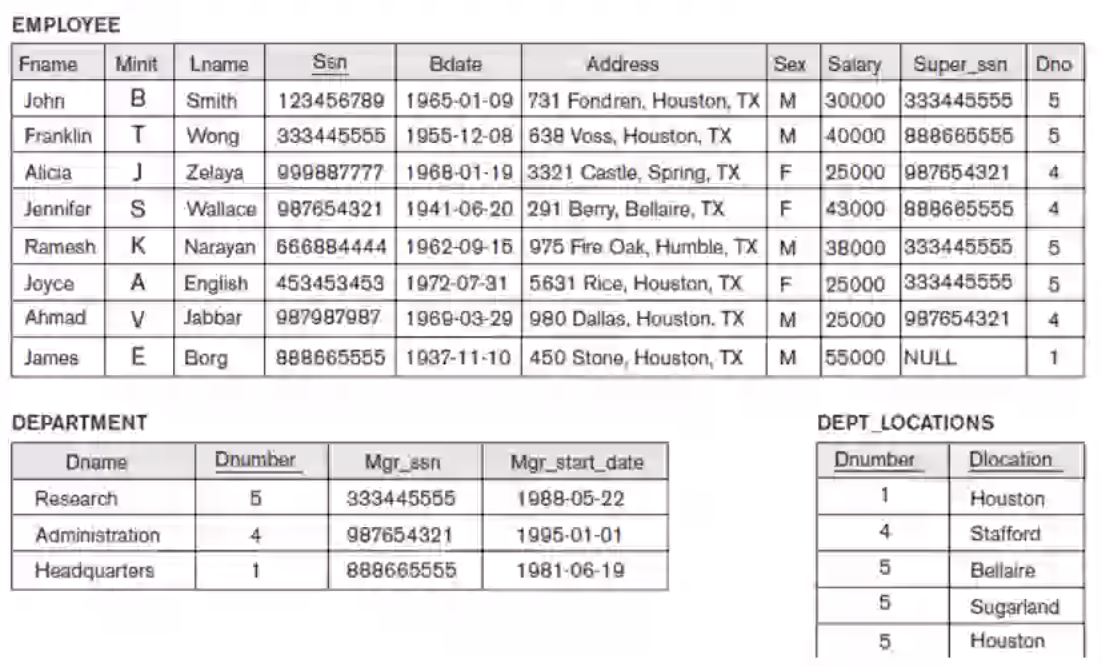
Which is populated with these data

• The basic set of operations for the relational model is known as the relational algebra
• These operations enable a user to specify basic retrieval requests
• The reult of a retreival is a new relation, which may have been formed from on or more relations.
• A sequence of relational algebra operations forms a relational algebra expression, whose result will also be a relation

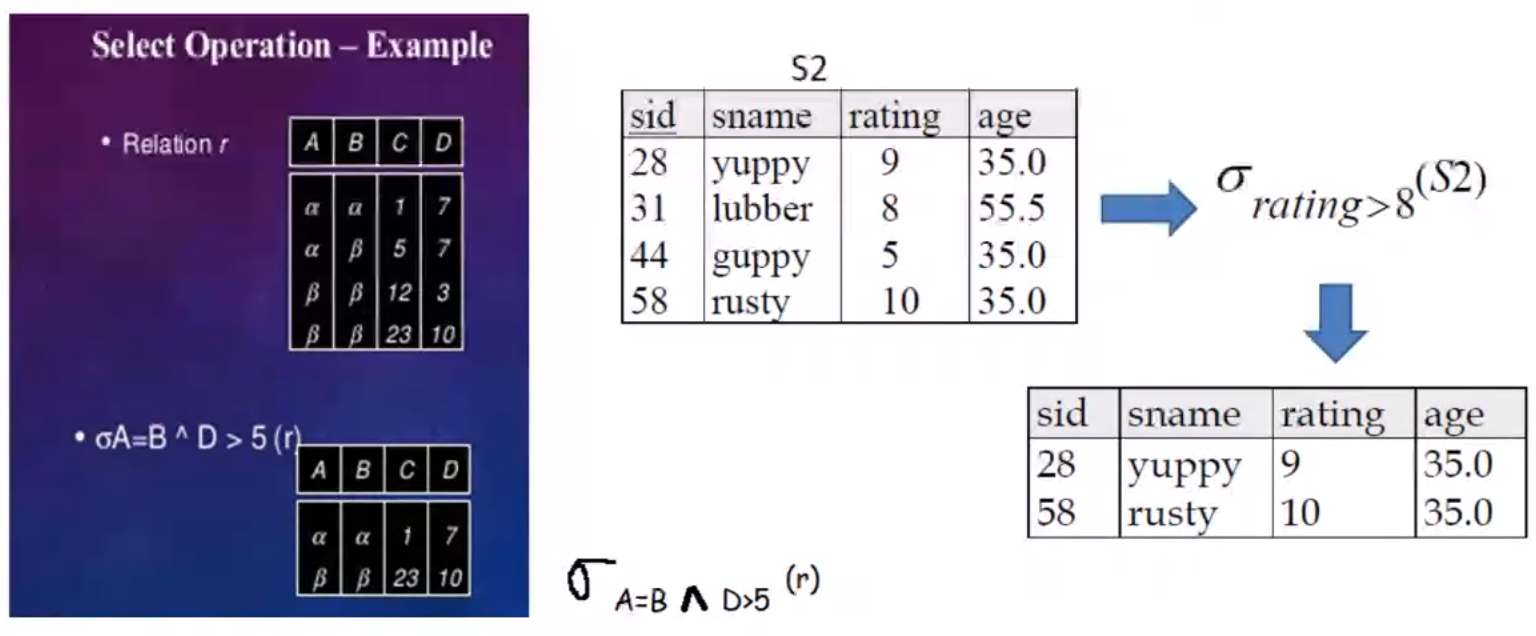
SELECT Operation

Select operation is used to select a subset of the tuples from a relation that satisfy a selection condition. The select operation is denoted by a sigma letter

\(\sigma_{DNO} = 4 (EMPLOYEE)\) (This represents all employees in department 4)
\(\sigma_{SALARY} \gt 30000 (EMPLOYEE)\) (This represents all employees in with salary greater than 30000)

Properties

• SELECT is commutative
• A cascade SEKLEECT operation may be applied in any order
  \(\sigma_{<condition\ 1>}(\sigma_{<condition\ 2>}(R))\) \(=\) \(\sigma_{<condition\ 2>}(\sigma_{<condition\ 1>}(R))\)
• A cascade SELECT operation can be
  \(\sigma_{<condition\ 1>}(\sigma_{<condition\ 2>}(\sigma_{<condition\ 3>}(R)))\) \(=\) \(\sigma_{<condition\ 2>}(\sigma_{<condition\ 3>}(\sigma_{<condition\ 1>}(R)))\)
• A cascade can also be written as:
  \(\sigma_{<condition\ 1>}(\sigma_{<condition\ 2>}(\sigma_{<condition\ 3>}(R)))\) \(=\) \(\sigma_{<condition\ 1>}(\sigma_{<condition\ 2>}(\sigma_{<condition\ 3>}(R)))\)

Example

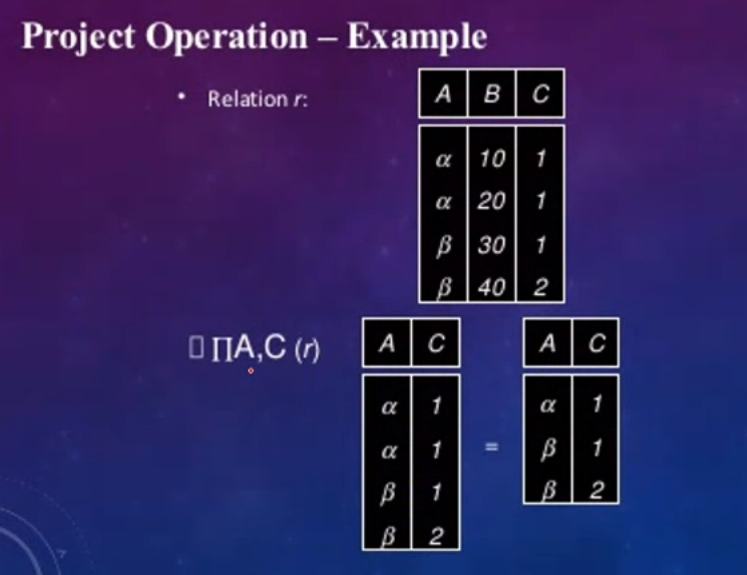
PROJECT Operation

This operation selects certain columns from the table and discards the rest. This is shown as the pi letter

\(\pi_{LNAME,\ FNAME,\ SALARY}(EMPLOYEE)\)

Properties

• The number iof tuples in the result of projection \(\pi_{<list>}(R)\) is always less or equal to the number of tuples in R
• If the list of attributes

Example

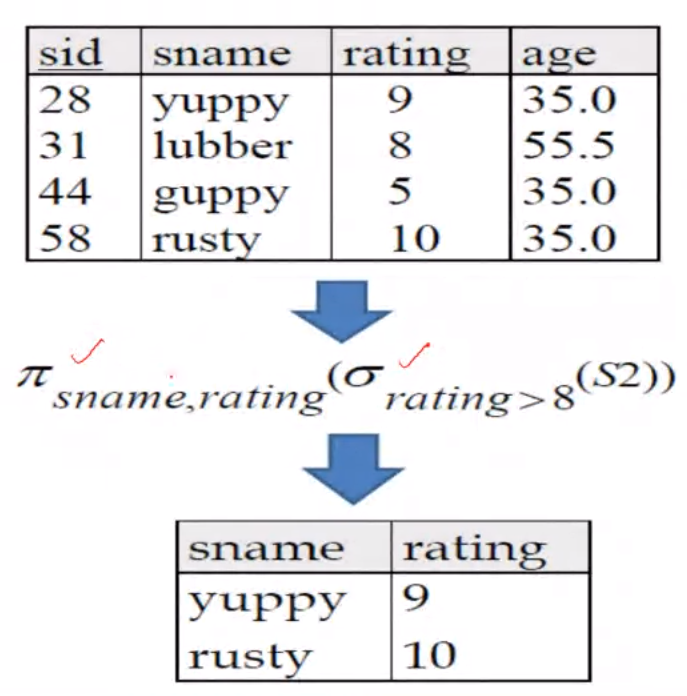
Combination of SELECT and PROJECT

TYPE COMPATIBILITY

• The operand relations must have the same number of attributes and the domains of the corresponding attributes must be compatible

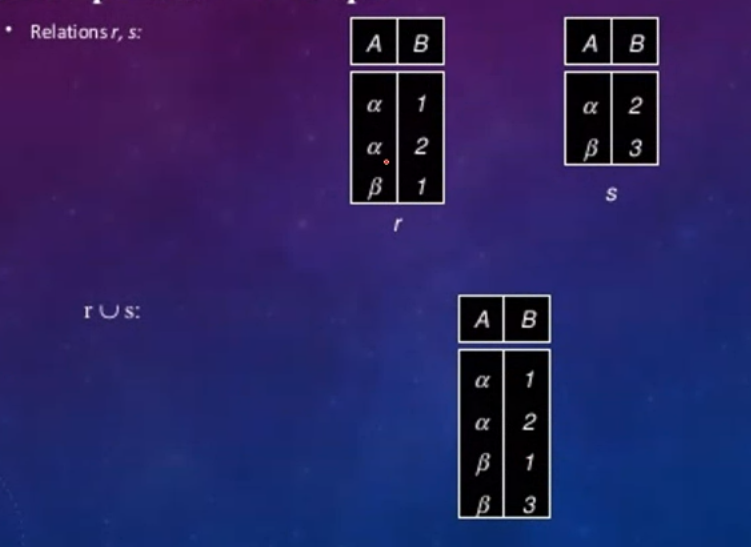
UNION Operation

Denoted as \(R \cup S\), means that all the tuples of \(R\) and \(S\) will be accumulated together and any duplicates are thrown away

Example

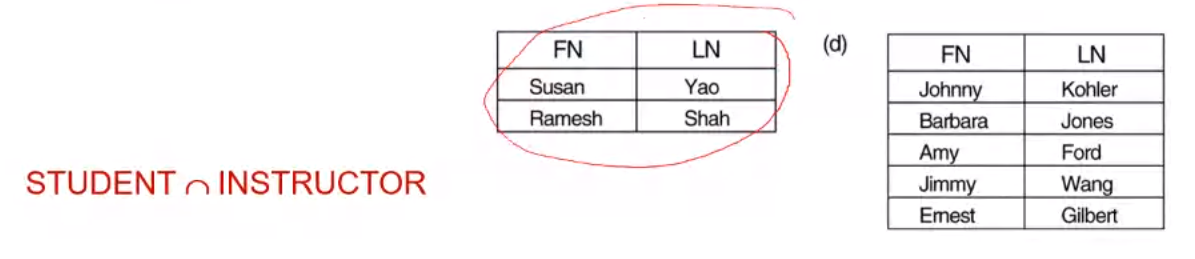
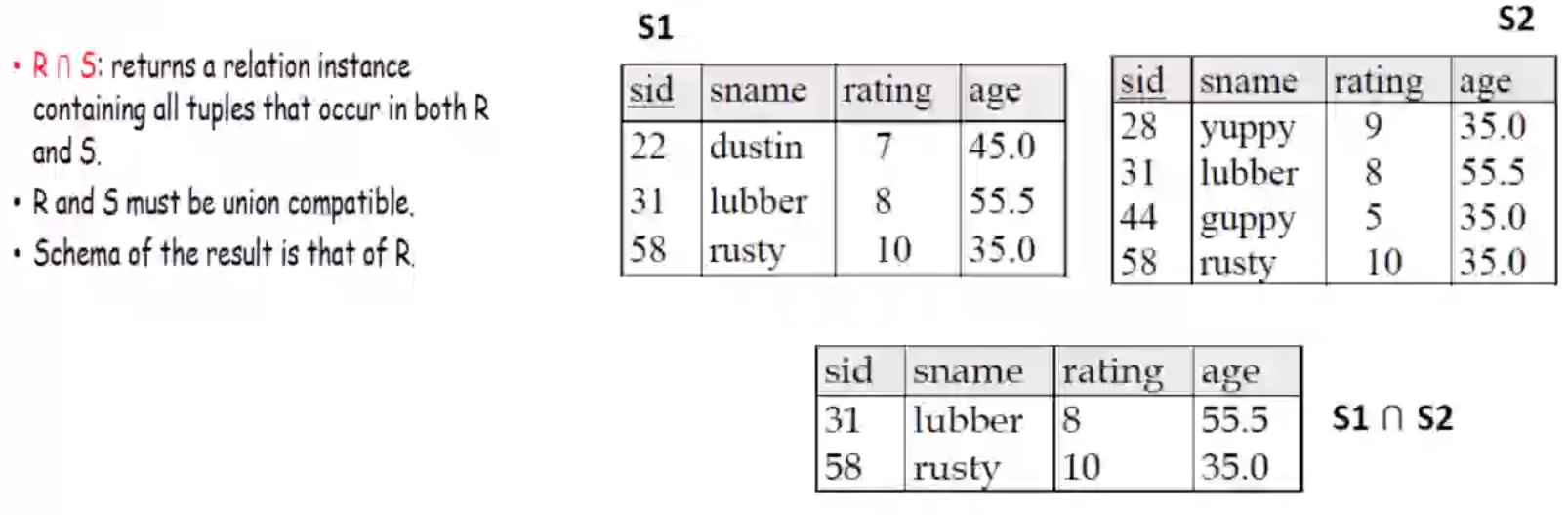
INTERSECTION Operation

Denoted as \(R \cap S\), means that common tuples of \(R\) and \(S\) will be accumulated together and others are thrown away

Examples

Consider the same example as the UNION operation, then intersection is:

SET DIFFERENCE Operation

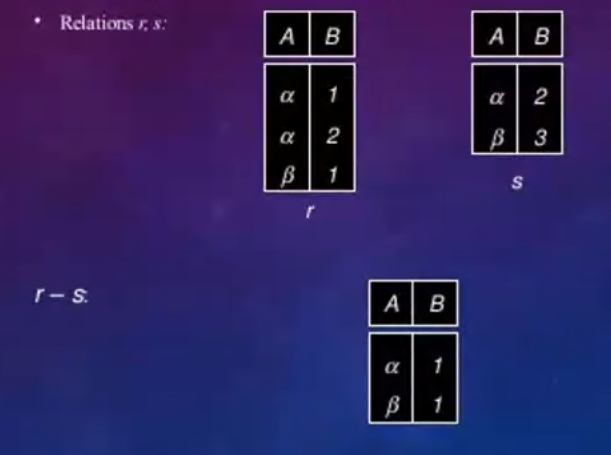
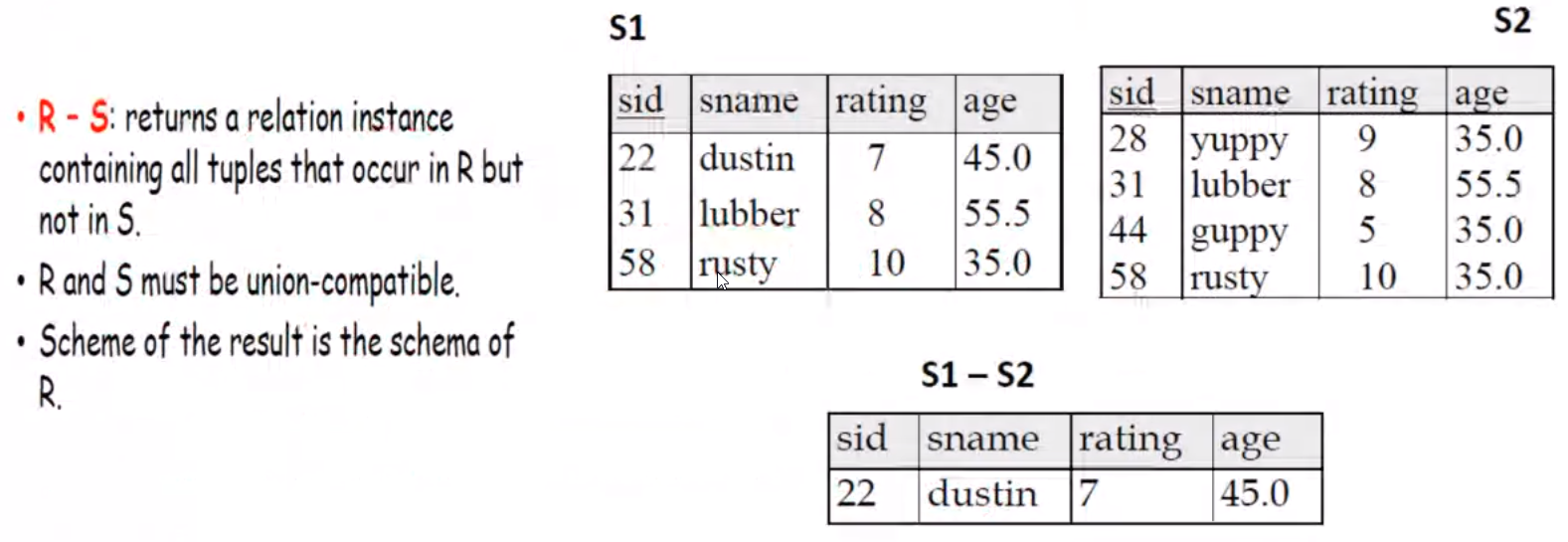
• The result of this operation denoted by \(R - S\) is a relation that includes all tuples that are in \(R\) but not in \(S\)
• Here order matters, meaning \(R - S\) need not be the same as \(S - R\)

Examples

Some properties for UNION, INTERSECTION and SET DIFFERENCE operations

\(R \cup S = S \cup R\)
\(R \cap S = S \cap R\)

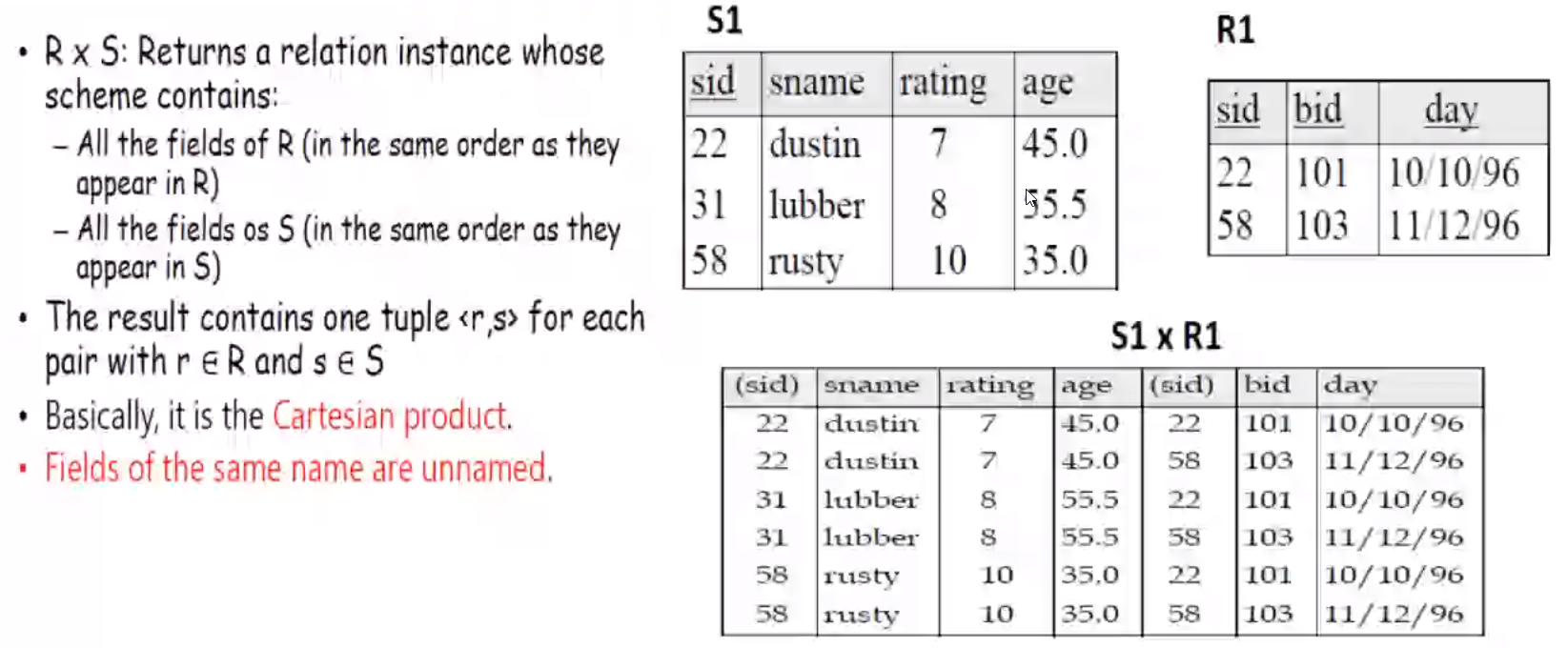
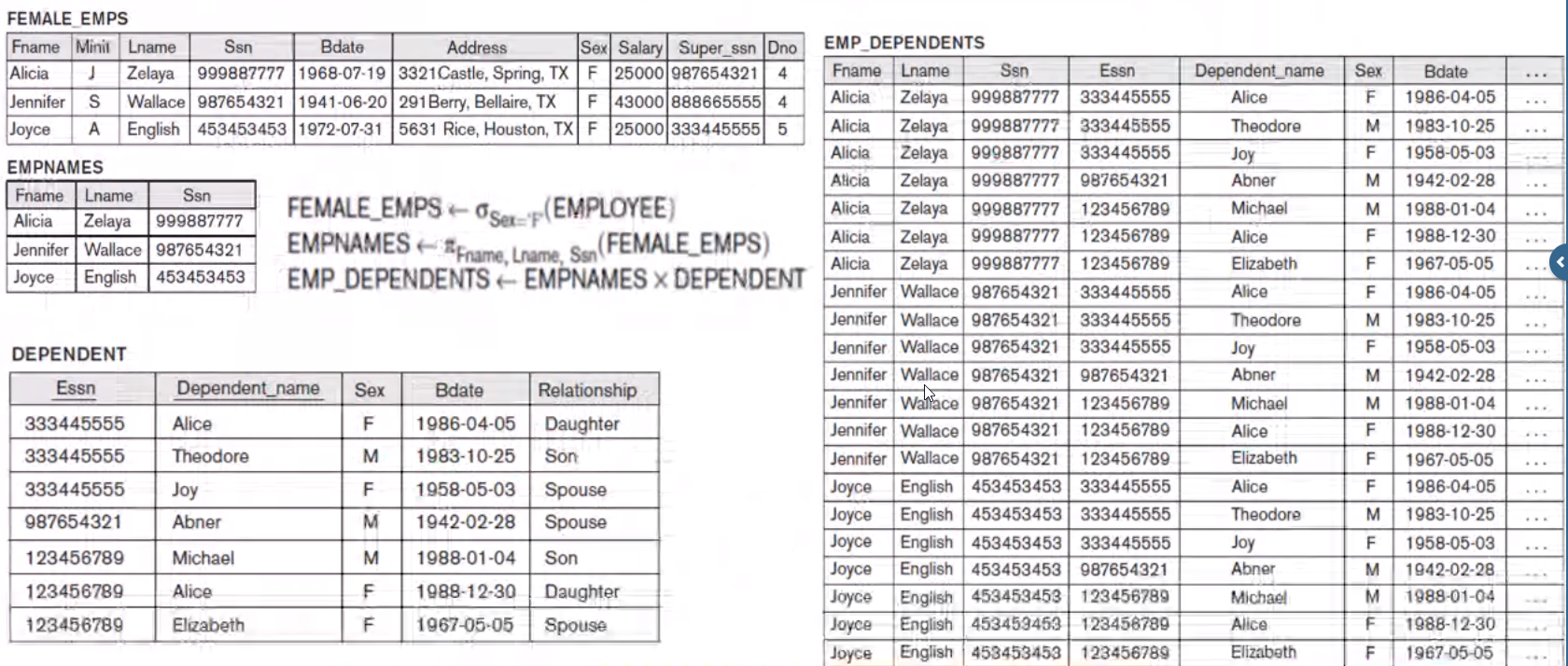
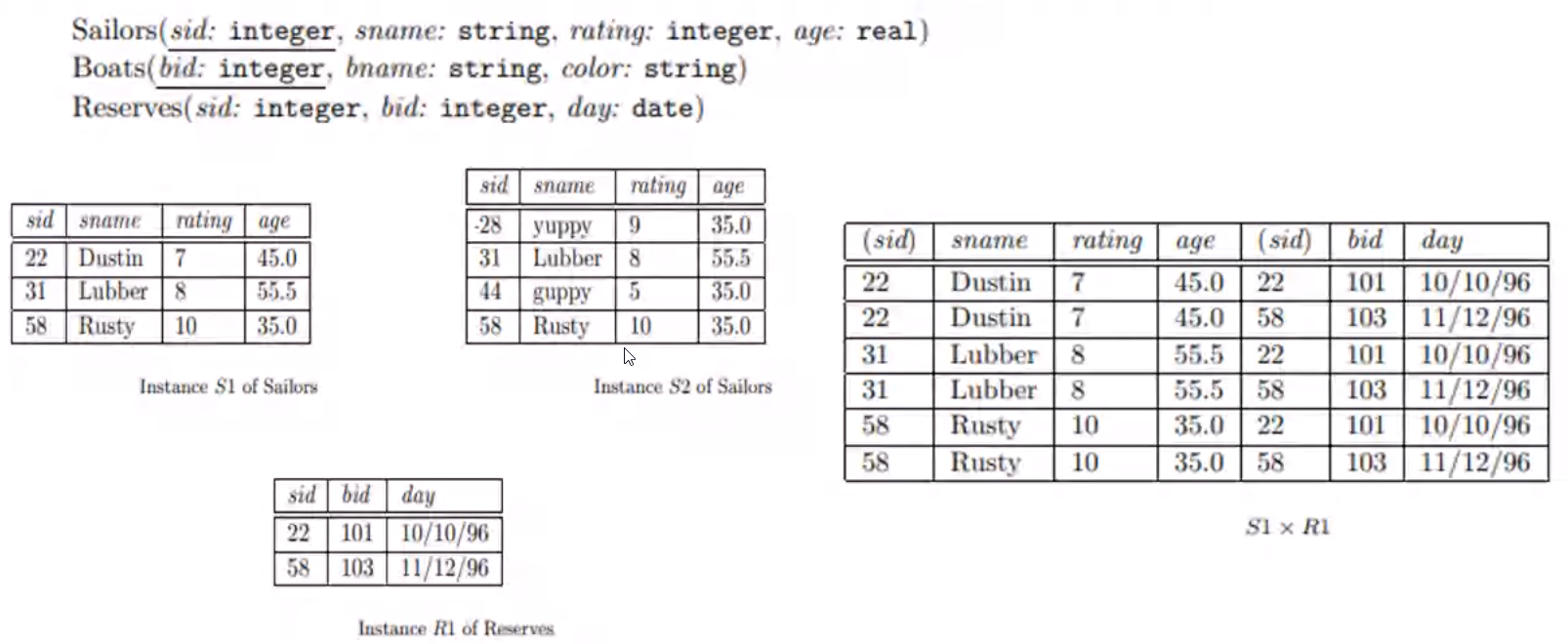
CARTESIAN (Cross Product) Operation

Cartesian product combines each and every row of the two relations. It is denoted by \(R x S\)

Examples

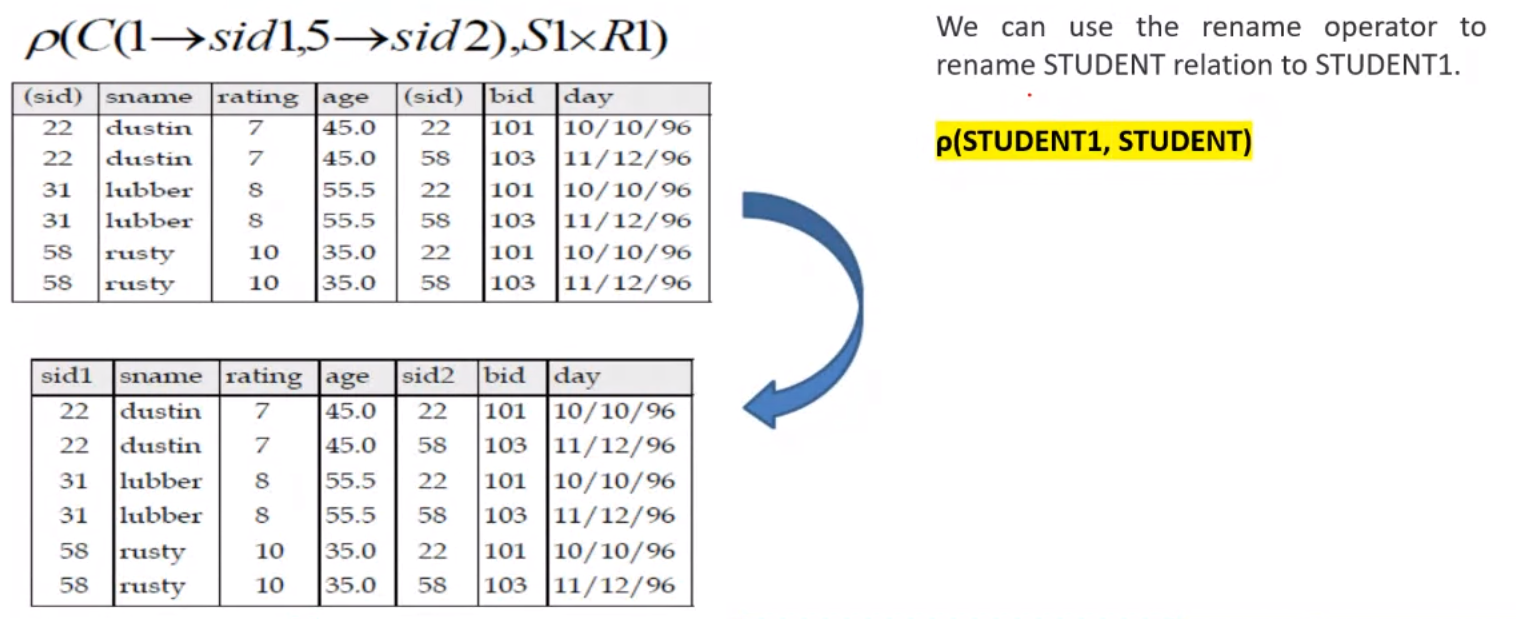
RENAME Operation

• Name conflicts can arise in some situations
  

Examples

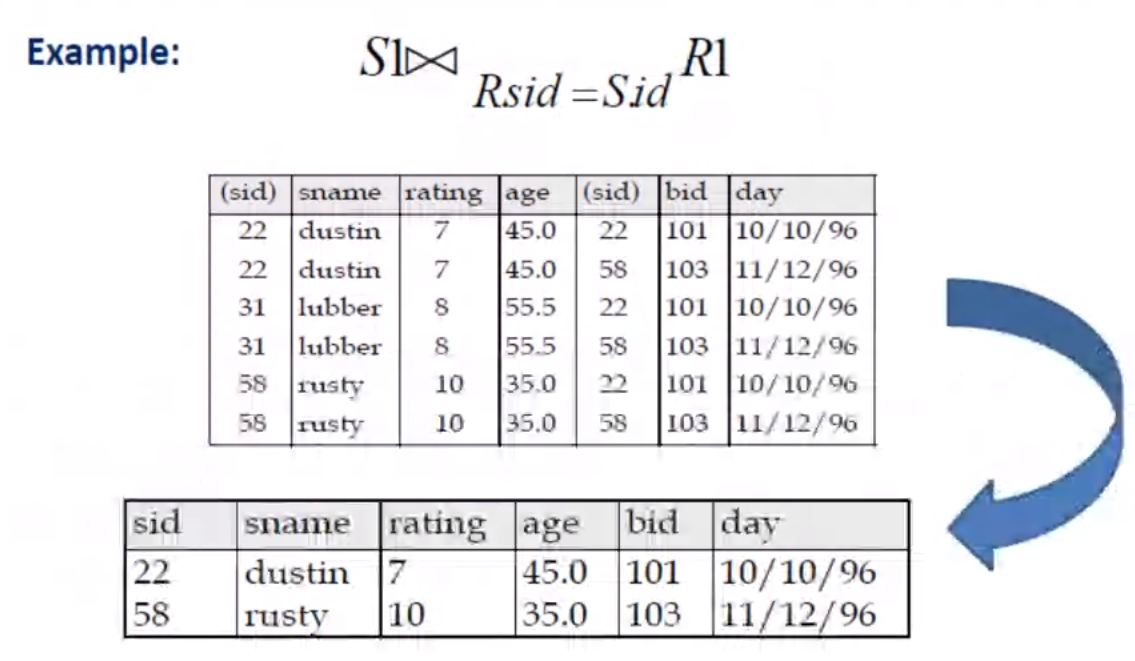
JOIN Operation

Sequence of CARTESIAN Operation followed by a SELECT

Types of JOIN Operations

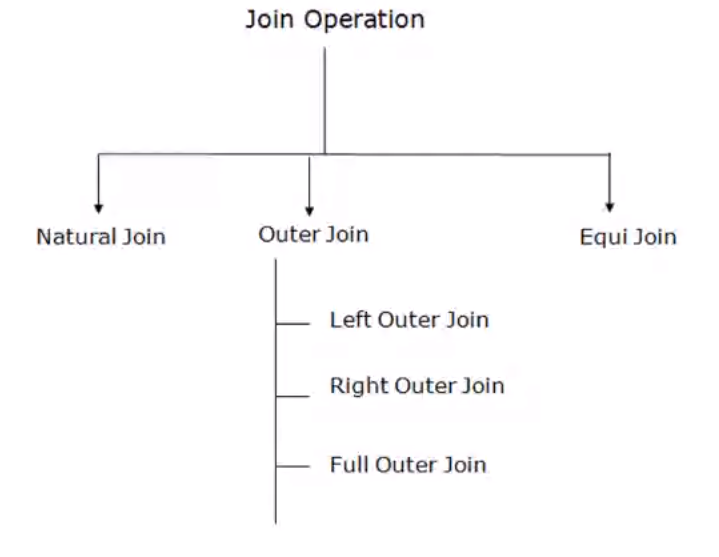
Conditional Join

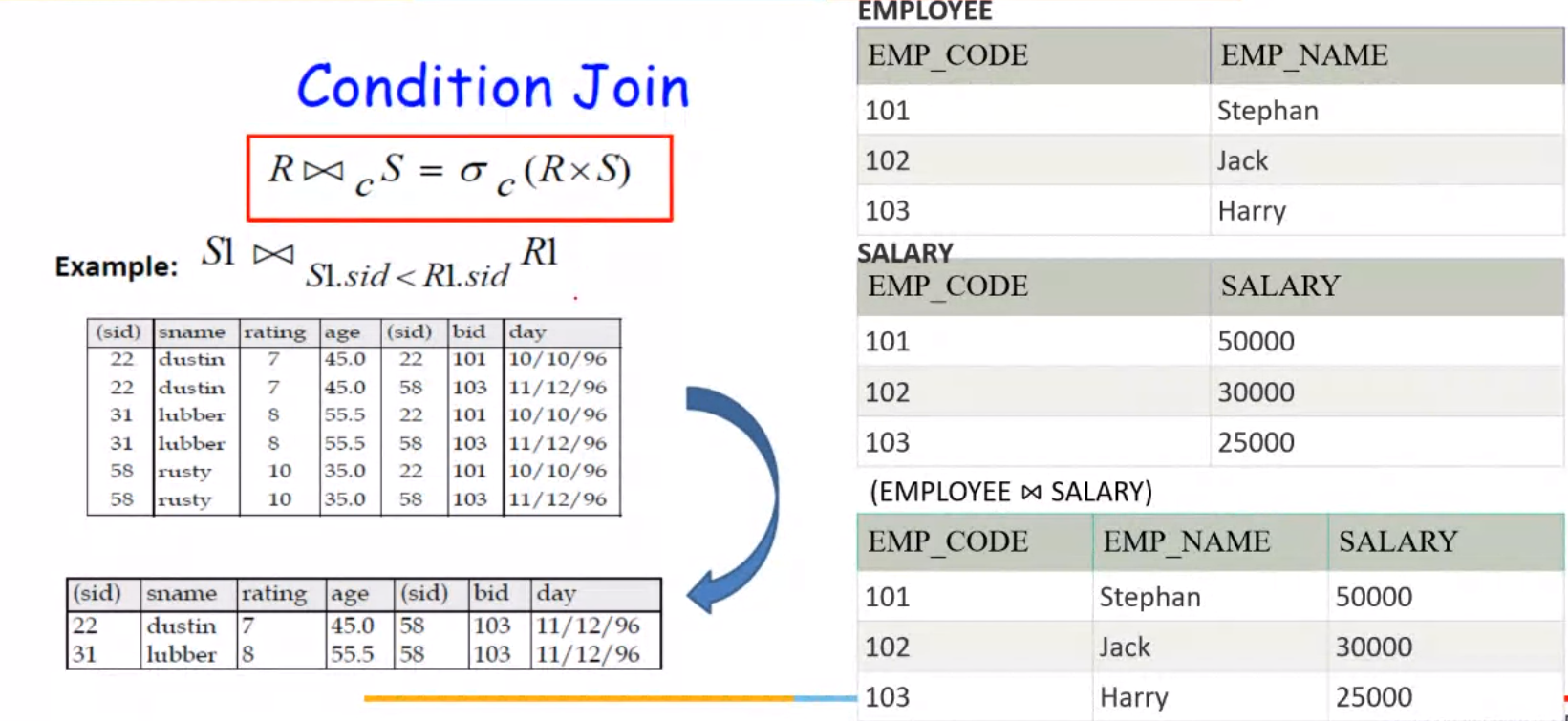
In the employee example the condition is \(EMPLOYEE.EMP\_CODE = SALARY.EMP\_CODE\)

Natural Join

denoted as \(*\)

Join such that the tuples are equal on all the common attribute names

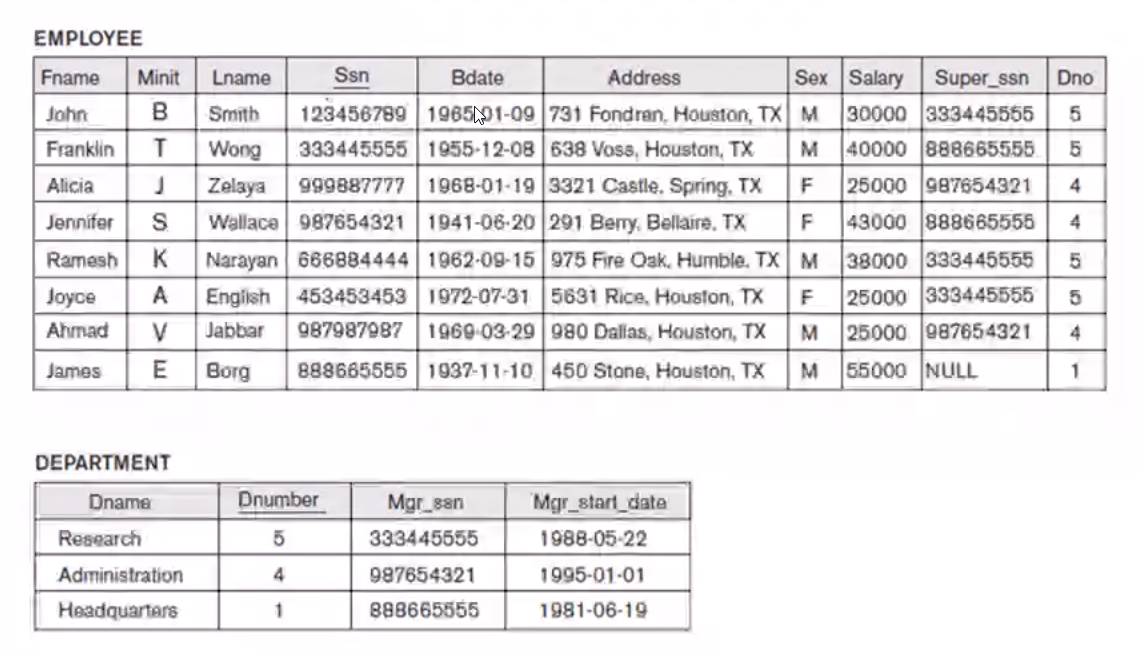
A Complete Example:

Equi Join

A join where the only comparison operator used is \(=\). In the result of an EQUIJOIN we always have one or more pairs

THETA Join

Apart from \(=\) all the other comparison operators are also used

OUTER Join

• Left Outer Join: Keeps every tuple in the first/left relation \(R\); if no matching tuple is found in \(S\), then attributes of \(S\) are given null values
  

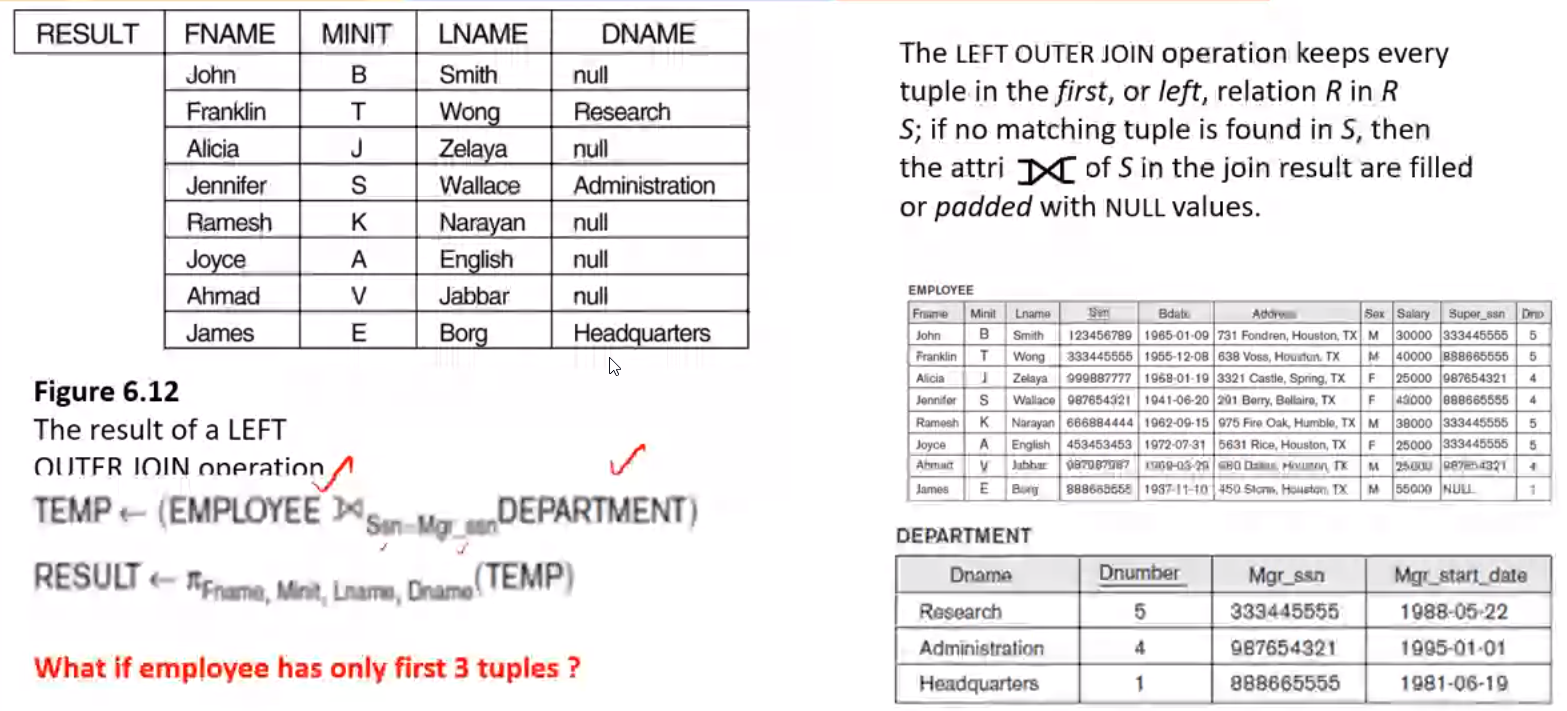
• Right Outer Join: Keeps every tuple in the second/right relation \(S\); if no matching tuple is found in \(R\), then attributes of \(R\) are given null values

• Full outer join: Keeps every tuple in both the relations \(R\) and \(S\) and the rest are padded with \(null\)

OUTER UNION Operation

---

Complete Set of Relational Operations

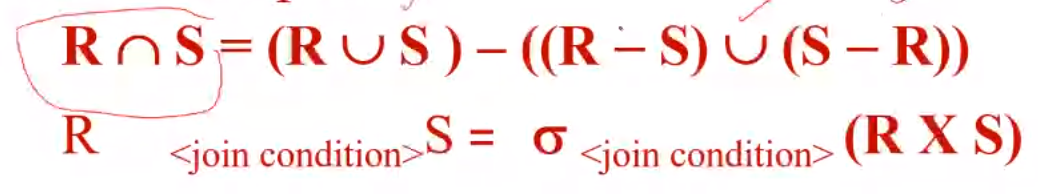
DIVISION Operation

denoted by \(\div\)

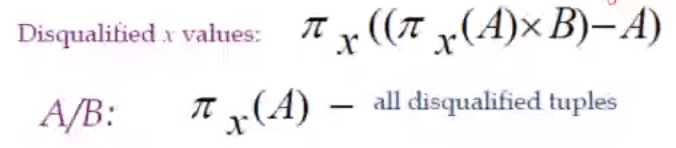
Examples

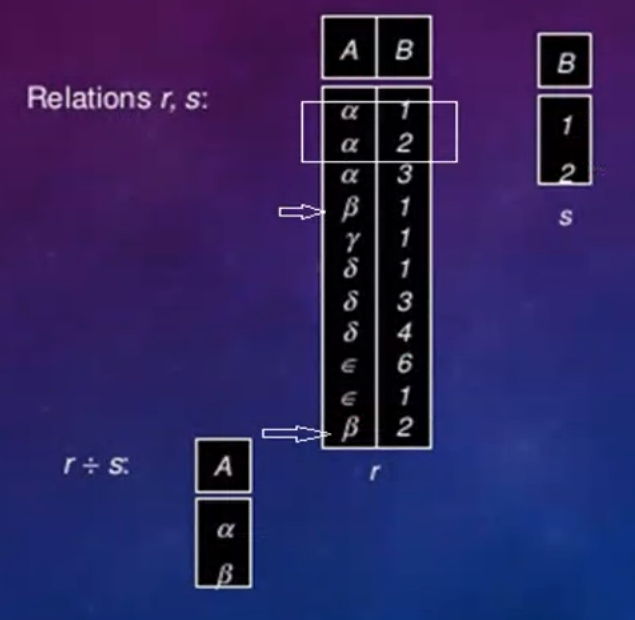
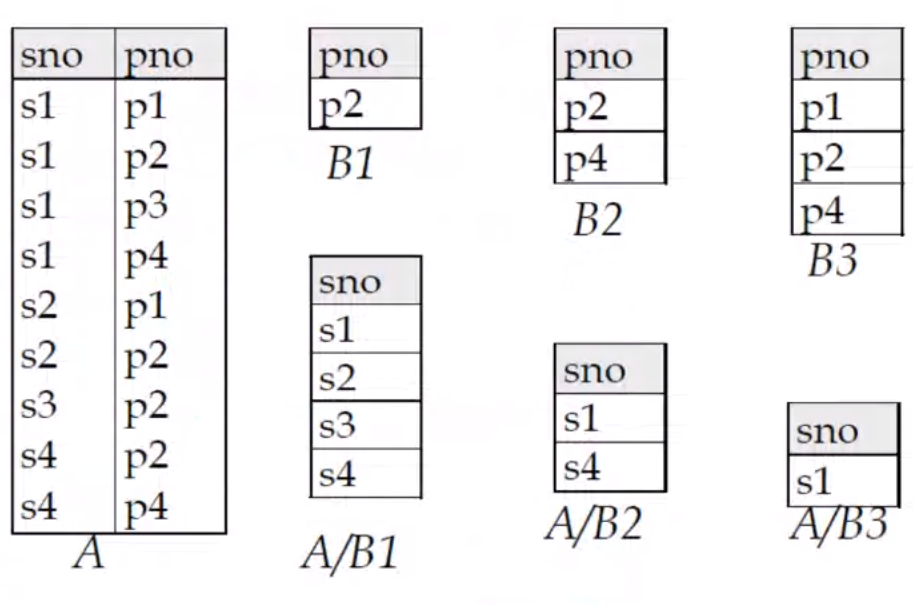
Another example

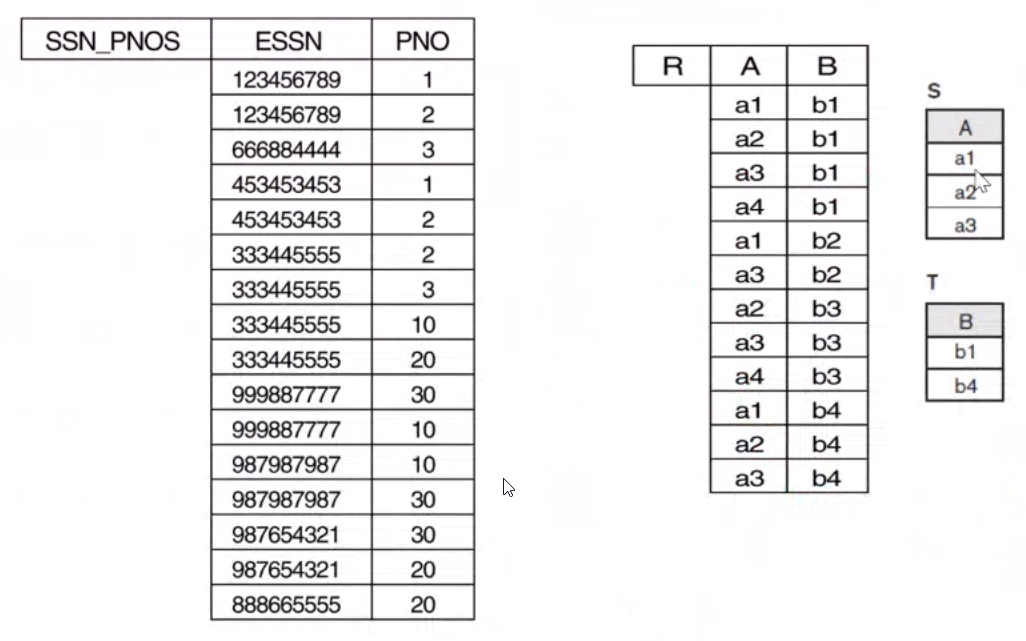
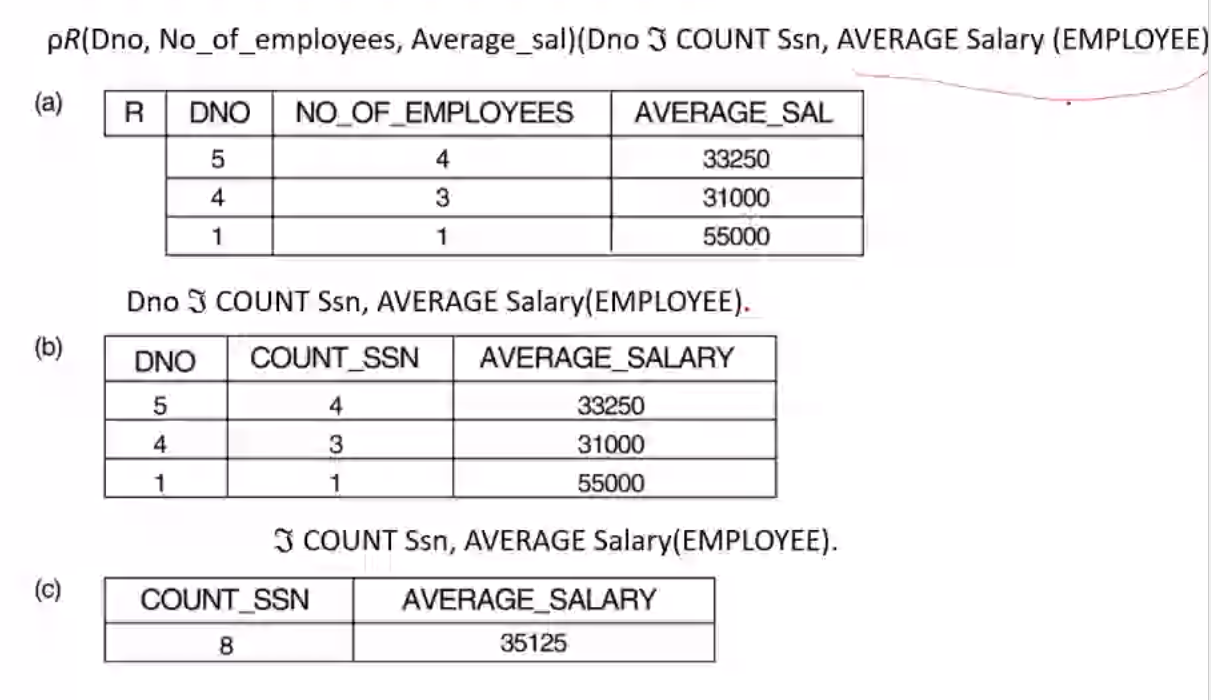
Aggregate Functions and Grouping Operation

---

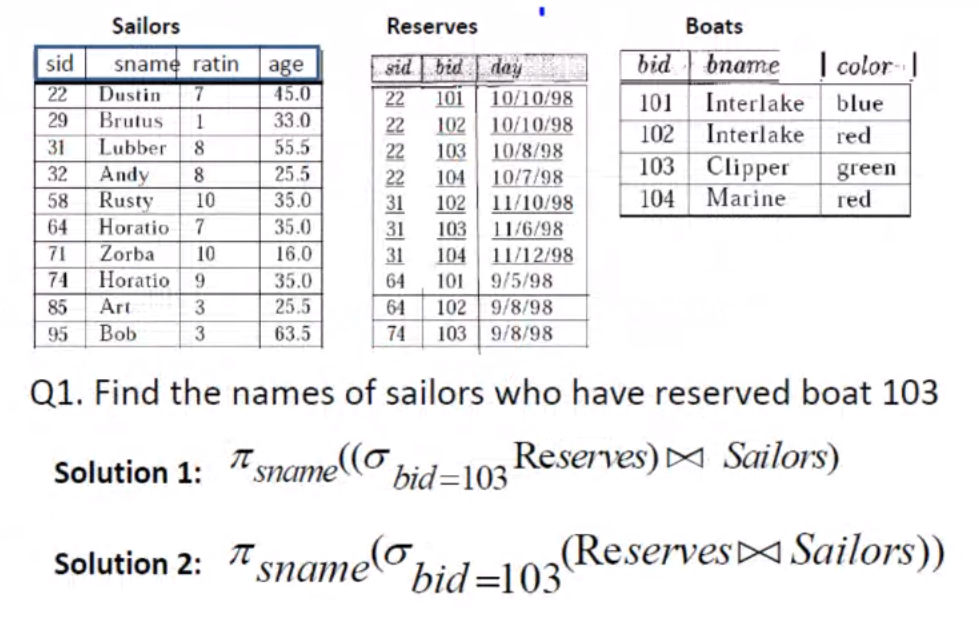
Tutorial Session

Post Lecture Notes

• Go through the SQL slides for the next week
• Go through the example problems in the book for relational algebra

---

Tags: !DatabaseDesignAndApplicationIndex