Week 6 (cont.)

Lecturer: Pritam Bhattacharya, BITS Pilani, Goa Campus

Date: 5/Sep/2021

Topics Covered

1. Quick Sort
   1. Steps Done
   2. Algorithm
      1. Pivot Function
      2. Quick Sort Function
   3. Algorithm Analysis
      1. Space Complexity
      2. Time Complexity

Quick Sort

Steps Done

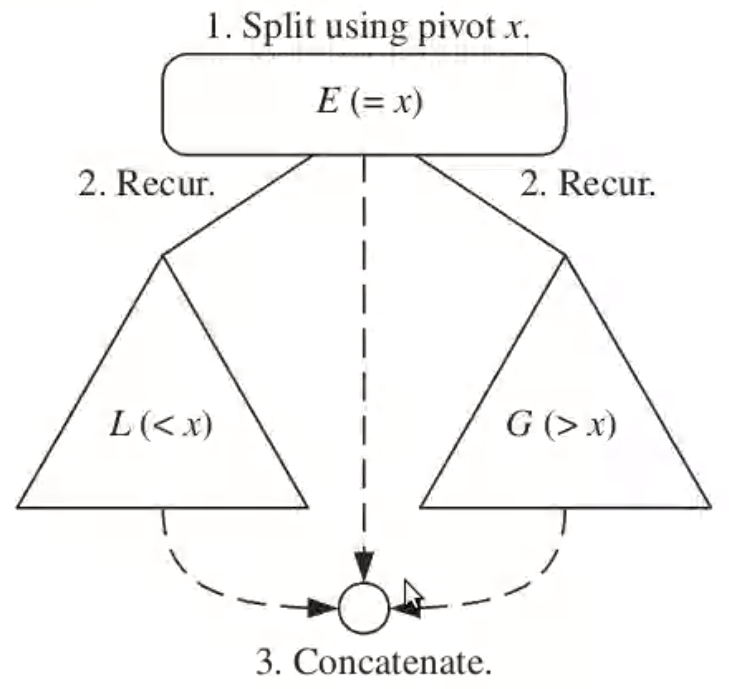
The actual sorting is done in a divide and conquer fashion denoted by the below steps:
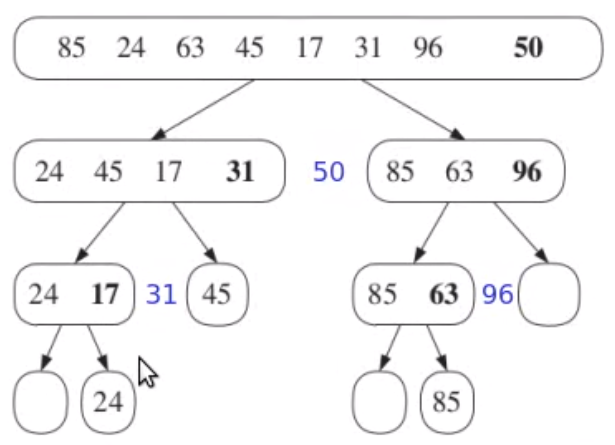
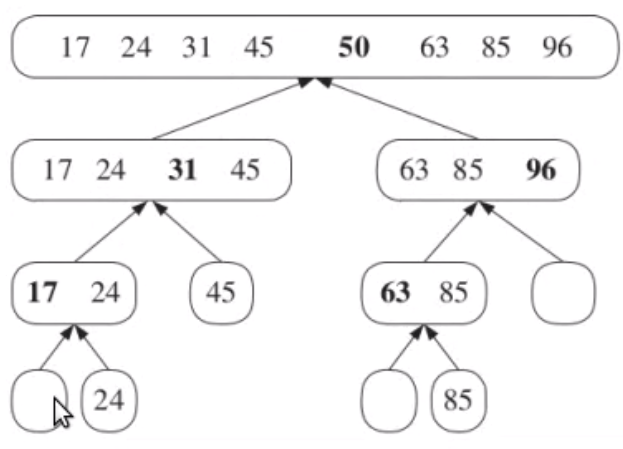
1. Divide: If \(S\) has zero or one element, return \(S\) immediately, it is already sorted, Otherwise pick a random element as a pivot element, and generate 3 parts:
1. \(L\) : The elements less than the pivot element
2. \(E\) : The element that is used as a pivot
3. \(G\) : The elements greater than the pivot element
2. Recur: Recursively sort the sequences \(L\) and \(G\)
3. Conquer: Concatenate the three sequences and return that

Algorithm

Pivot Function

partition(arr, low, high)
    Input: An array of integers arr the lower index for the partition in the array and high the upper index
    Ouput: pi, Partitioning index, the index where the pivot is placed 

    pivot = arr[high]
    i = (low - 1)
    for(j = low; j <= high - 1; j++) then
        if arr[j] < pivot then
            i++
            arr[i] <-> arr[j]
    arr[i + 1] <-> arr[high]
    return (i + 1)

Quick Sort Function

sort(arr, low, high)
    Input: An array of integers arr the lower index for the partition in the array and high the upper index
    Ouput: pi, Partitioning index, the index where the pivot is placed

    if low < high then
        pi = partition(arr, low, high)
        sort(arr, low, pi - 1)
        sort(arr, pi + 1, high)

Algorithm Analysis

Space Complexity

The in place algorithm does not take any extra space so we can say the space complexity is \(\mathcal{O}(1)\)

Time Complexity

The partition function performs a single loop on the array elements, so the total number of operations done on a given level is proportional to n, so the time complexity here is \(\mathcal{O}(n)\).

In the best case, where the partition was balanced:
The sort function recursively calls sort by dividing the array into two segments and a pivot, so the size reduces at the rate of \(log\ n\) so the time complexity is \(\mathcal{O}(log\ n)\).
The total time complexity is: \(\mathcal{O}(n\ log\ n)\)

In the worst case, where the partition is not balanced

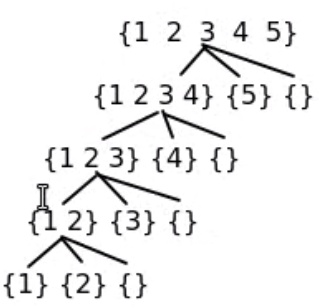
The sort function would end up creating \(n - 1\) levels, making the total time complexity as \(\mathcal{O}(n^2)\)

The reason why this sort is called Quick sort is because, the worst case happens very rarely and even if it does it can be fixed with a simple check to see if an array is already sorted.

---

Tags: !DatastructuresAndAlgorithmsIndex