Skip to content

Week 2#

Lecturer: G Venkiteswaran, Faculty for BITS Pilani
MailBadge
Date: 01/Aug/2021

Topics Covered#

  1. Vector Norms
    1. Common Norms
    2. Equivalence of Norms
  2. Matrix Norms
  3. Solution of Linear systems
  4. Gauss elimination methods
    1. Pitfalls of Gauss Elimination Algorithms
      1. Division By Zero
      2. Round-off Errors
    2. Operations Count for Gaussian Elimination
  5. Ill Conditioned Systems
    1. Condition Number

Vector Norms#

A function \(|| . || : R^n \rightarrow R\) is a vector norm if it has the following properties:
1. \(||x|| \ge 0\) for any vector \(x \in R^n\), and \(||x|| = 0\) if and only if \(x = 0\).
2. \(||\alpha x|| = |\alpha|\ ||x||\) for any vector \(x \in R^n\), and any scalar \(\alpha \in R\).
3. \(||x+y|| \le ||x|| + ||y||\) for any vectors \(x,\ y \in R^n\). This property is called the triangle inequality (Sum of two sides is greater than the third)
4. Also to be noted is if the dimension value \(n=1\) then the modulus value function (\(|x|\)) is a vector norm. (where mod function is \(|x| = \max(x,-x)\))

Common Norms#

The most commonly used vector norm is belong to the family of \(l_p\) norms, which are defined by:

\[||x||_p = \begin{equation}(\sum_{i = 1}^{n}|x|^p)^{1/p}\end{equation}\]

The following \(l_p\) norms are more used than others:
1. \(p=1:\ The\ l_1\ norm\ ||x||_1 = |x_1| + |x_2| + \dots + |x_n|\)
2. \(p=2:\ The\ l_2\ norm\ or\ Euclidean\ norm ||x||_2 = \sqrt{x_1^2 + x_2^2 + \dots + x_n^2} = \sqrt{x^Tx}\)
3. \(p=1:\ The\ l_\infty\ norm\ ||x||_{\infty} = \max_{1\le i\le n}|x_i|\)

Equivalence of Norms#

We say that two vector norms are equivalent if there exists constants \(C_1\) and \(C_2\), that are independent of \(x\), such that for any vector \(x \in R^n\)

\[C_1||x||_\alpha \le ||x||_\beta \le C_2||x||_\alpha\]

Remember that the above equation does not show any relation between \(C_1\) or \(C_2\) or \(\alpha\) or \(\beta\)

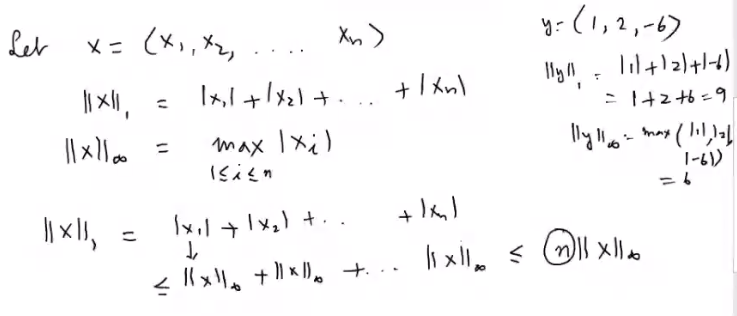
Pasted image 20210801153631.png
Consider the above example, we take the two forms of \(l_p\) norms, the \(l_1\) and the \(l_\infty\).
You can see that each term of \(||x||_1\) is \(\le \ ||x||_\infty\) hence we can say that the total sum \(||x||_1 \le n||x||_\infty\).
This shows the equivalence of \(l_1\) and \(l_\infty\) norm.

Matrix Norms#

Some commonly used matrix norms are:
1. Matrix norm corresponding to vector \(1\)-norm is maximum modulus/absolute column sum:

\[||A||_1 = \max_{j}(\begin{equation} \sum_{i=1}^{n} |a_{ij}| \end{equation})\]

You can see that we take the maximum of the absolute sum of the columns

  1. Matrix norm corresponding to vector \(\infty\)-norm is maximum modulus/absolute column sum:
\[||A||_\infty = \max_{i}(\begin{equation} \sum_{j=1}^{n} |a_{ij}| \end{equation})\]

You can see that we take the maximum of the absolute sum of the columns

  1. Matrix norm corresponding to vector \(2\)-norm is given as:
\[||A||_2 = ||A||_F = \sqrt{\sum_{i=1}^{M}\sum_{j=1}^{N} |a_{ij}|^2}\]

Question asked: What is the significance of a norm for a matrix?

Visualizing the above through Octave commands:

>> A = [2,1,1;3,2,1;-2,0,1]
A =

   2   1   1
   3   2   1
  -2   0   1

>> norm(A, 1)
ans = 7
>> norm(A, 'inf')
ans = 6
>> norm(A, 'fro')
ans = 5
>> norm(A, 2)
ans = 4.6758

Question to ask: if \(||A||_2 = |A||_F\) why are the results different in the above octave result?

Solution of Linear systems#

Matrix form of Linear Systems
We can take m linear equations and write them as a single Vector equation like

\[Ax=b\]
  • Where coefficient matrix \(A = [a_{jk}]\) is the \(m\ x\ n\) matrix
  • Where all the variables are in the vector \(x = [x_k]\) with size \(n\ x\ 1\)
  • Where all the constants are in vector b \(b = [b_j]\) with size \(m\ x\ 1\)

Gauss Elimination#

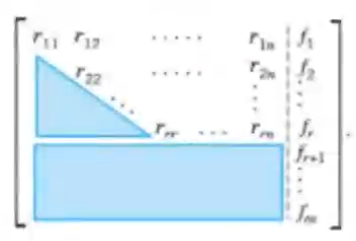
Pasted image 20210801191603.png
Consider the above image, at the end of gauss elimination, the row echelon form would hold a rank say \(r\), then we can say:
1. The matrix is a upper triangular form
2. The first \(r\) rows are non zero
3. Exactly \(m-r\) rows would be zero rows
4. The rhs can have two possibilities:
1. The rhs has exactly \(m-r\) zero rows: This means there is atleast one solution for the linear system of equations
2. The rhs has less than \(m-r\) zero rows: This means the equations are inconsistent
5. If the system is consistent and the \(r = n\) then there is exactly one solution
6. In case of infinitely many solutions, take arbiterary values for \(x_{r+1},\dots x_n\), then solve the \(r\)th equation for \(x_r\), then the \((r-1)\)st equaation for \(x_{r-1}\), and so on up the line till the solutions are found
7. The complexity for calculating this is \(O(n^3)\), where \(n\) is the number of rows

Pasted image 20210801193538.png

Pitfalls of Gauss Elimination Algorithms#

Division By Zero#

It is possible that in the above considered example, the denominator can end up being a zero value. For example consider the example below:
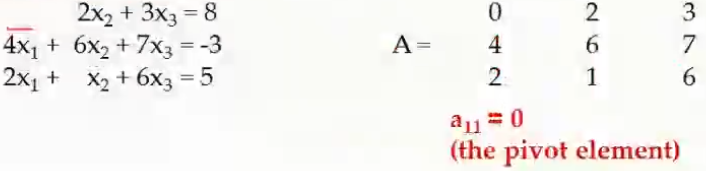
Pasted image 20210801194614.png
Here the coefficient of \(x_1\) in the first equation is 0, hence to avoid the above issue we can interchange rows \(R_1 \rightarrow R_2\). This is called pivoting and that will make it easier to bring about the REF form for the matrix.

Round-off Errors#
  • Because computers can carry limited number of significant figures, round off errors will occur and they will propagate for every iteration.
  • This problem becomes very apparent when the number of equations become very large.
  • To avoid this one must use double-precision numbers. Albeit it being slow, the result will be more correct

Operations Count for Gaussian Elimination#

The details for the operation counts for several operations done is explained in the page here: GaussianEliminationPython#Operations Count

Ill Conditioned Systems#

Consider the following system of linear equations:
\(x_1 + 2x_2 = 10\)
\(1.1x_1 + 2x_2 = 10.4\)
We get the values of \(x_1 = 4.0\) and \(x_2 = 3.0\)

If let us say that when someone modeled this equation they had made a miscalculation leading to changing one of the coefficients of \(x_1\) from \(1.1\) to \(1.05\) making the above system of equations as follows:
\(x_1 + 2x_2 = 10\)
\(1.05x_1 + 2x_2 = 10.4\)
We get the values of \(x_1 = 8.0\) and \(x_2 = 1.0\)

From the above two results you can see that there is a big variance in the results when there is a small change in the coefficients, such system of equations are said to be ill conditioned

Condition Number#

The condition number is a metric that is used to see if a system of equations is ill informed or not. Condition number of a non singular matrix A is defined as:

\[\kappa(A) = ||A|| ||A^{-1}||\]

By convention \(\kappa(A) = \infty\) if \(A\) is singular (A matrix whose determinant is 0, and hence has no inverse)

Example:

\[A = \begin{bmatrix}2 & -1 & 1\\1 & 0 & 1\\3 & -1 & 4\end{bmatrix},\ ||A||_1 = 6,\ ||A||_\infty = 8\]
\[A^{-1} = \begin{bmatrix}0.5 & 1.5 & -0.5\\-0.5 & 2.5 & -0.5\\-0.5 & -0.5 & 0.5\end{bmatrix},\ ||A^{-1}||_1 = 4.5,\ ||A^{-1}||_\infty = 3.5\]
\[\kappa_1(A) = 6 * 4.5\]
\[\kappa_\infty(A) = 8 * 3.5\]
  • Once conditions are calculated, we can say that whenever the condition number is in the range of 4 to 5 then they are well informed but if the condition is around a 100 or so then they are more ill conditioned in nature.
  • There is no clear distinction between well informed and ill informed system of equations

Tags: !MathematicalFoundationsIndex