Week 5#
Lecturer: Barsha Mitra, BITS Pilani, Hyderabad Campus
Date: 28/Aug/2021
Topics Covered#
- Message Ordering (cont.)
- Birman-Schiper-Stephenson Protocol
- \(P_i\) sends a message \(m\) to \(P_j\)
- \(P_j\) receives a message \(m\) to \(P_i\)
- Birman-Schiper-Stephenson Protocol
- Distributed Mutual Exclusion
- Types of Approaches
- Quorum Based
- Requirements of Mutual Exclusion Algorithms
- Performance Metrics
- Lamport's Algorithm
- Requesting the Critical Section
- Executing the Critical Section
- Releasing the Critical Section
- Example Problem
Message Ordering (cont.)#
Birman-Schiper-Stephenson Protocol#
- \(C_i\) = Vector clock of \(P_i\)
- \(C_i[j]\) = \(j^{th}\) element of \(C_i\)
- \(tm\) = Vector timestamp for message \(m\), stamped after local clock is incremented.
- NOTE, we also assume that all messages taking part in this algorithm is a broadcast
\(P_i\) sends a message \(m\) to \(P_j\)#
- \(P_i\) increments \(C_i[i]\)
- \(P_i\) sets the timestamp \(tm = C_i\) for message \(m\)
\(P_j\) receives a message \(m\) to \(P_i\)#
- When \(P_j (j \ne i)\) reveives \(m\) with timestamp \(tm\), it delays message delivery until:
- \(C_j[i] = tm[i] - 1\), \(P_j\) has received all preceding messages sent by \(P_i\)
- \(\forall k \le n\) and \(k \ne i\), \(C_j[k] \ge tm[k]\), P_j has received all the messages that were received at \(P_i\) from other processes before \(P_i\) sent \(m\)
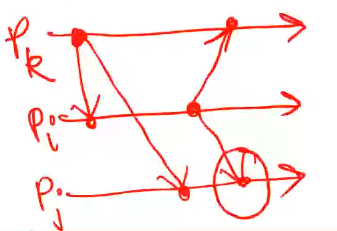
Here we need to check if \(P_j\) also received \(P_k\) message before message from \(P_i\) is processed
- When \(m\) is delivered to \(P_j\), update \(P_j\)'s vector clock, \(\forall i, C_j[i] = max(C_j[i], tm[i])\)
- Check buffered messages to see if any can be delivered
Example Problem#
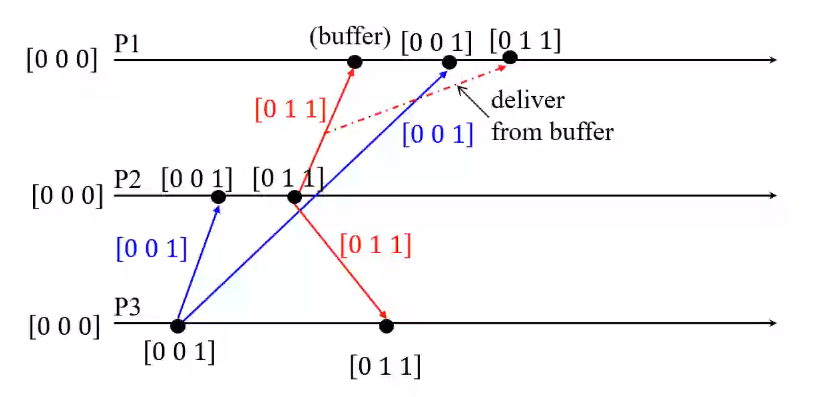
\(P_3\) executes a broadcast
- \(C_3 = [0, 0, 1]\)
- \(tm_1 = [0, 0, 1]\)
\(P_2\) receives message \(m_1\)
- \(C_2 = [0, 0, 0]\)
- Condition checks:
1. \(C_2[3] = tm_1[3] - 1\) is TRUE
2. \(C_2[i] \ge tm_1[i]\) \(\forall i \le n\) and \(i \ne 3\) is TRUE
- \(C_2[i] = max(C_2[i], tm_1[i]), \forall i\)
- \(C_2 = [0, 0, 1]\)
\(P_2\) sends message \(m_2\)
- \(C_2 = [0, 1, 1]\)
- \(tm_2 = [0, 1, 1]\)
\(P_3\) receives message \(m_2\)
- \(C_3 = [0, 0, 1]\)
- Condition checks:
1. \(C_3[2] = tm_2[2] - 1\) is TRUE
2. \(C_3[i] \ge tm_2[i]\) \(\forall i \le n\) and \(i \ne 2\) is TRUE
- \(C_3[i] = max(C_3[i], tm_2[i]), \forall i\)
- \(C_3 = [0, 1, 1]\)
\(P_1\) receives message \(m_2\)
- \(C_1 = [0, 0, 0]\)
- Condition checks:
1. \(C_1[2] = tm_2[2] - 1\) is TRUE
2. \(C_1[i] \ge tm_2[i]\) \(\forall i \le n\) and \(i \ne 2\) is FALSE
- \(m_2\) is added to BUFFER
\(P_1\) receives message \(m_1\)
- \(C_1 = [0, 0, 0]\)
- Condition checks:
1. \(C_1[3] = tm_1[3] - 1\) is TRUE
2. \(C_1[i] \ge tm_1[i]\) \(\forall i \le n\) and \(i \ne 3\) is TRUE
- \(C_1[i] = max(C_1[i], tm_1[i]), \forall i\)
- \(C_1 = [0, 0, 1]\)
Deliver \(m_2\) from BUFFER to \(P_1\)
- \(C_1 = [0, 0, 1]\)
- Condition checks:
1. \(C_1[2] = tm_2[2] - 1\) is TRUE
2. \(C_1[i] \ge tm_2[i]\) \(\forall i \le n\) and \(i \ne 2\) is TRUE
- \(C_1[i] = max(C_1[i], tm_1[i]), \forall i\)
- \(C_1 = [0, 1, 1]\)
NOTE, in the exam make sure that all the above steps are also written in the paper, annotating the diagram alone will lead to getting partial marks
Distributed Mutual Exclusion#
Types of Approaches#
- Token based
- Assertion based
- From Recorded Lecture
- Quorum based
Quorum Based#
- Each site requests permission to execute the CS from a subset of sites called quorum
- Quorums are formed in such a way that when two sites concurrently request access to the CS
- At least one site receives both the requests
- This site is responsible to make sure that only one request executes the CS at any time
Requirements of Mutual Exclusion Algorithms#
- Safety Property: At any instant, only one process can execute the CS
- Liveness Property: A site must not wait indefinitely to execute the CS while other sites are repeatedly executing the CS
- Fairness:
- Each process gets a fair chance to execute the CS
- CS execution requests are executed in order of their arrival time
- Time is determined by a logical clock
Performance Metrics#
From Recorded lectures
Lamport's Algorithm#
- Every site \(S_i\) keeps a queue, \(request\_queue_i\)
- \(request\_queue_i\) contains mutual exclusion requests ordered by their timestamps
- FIFO
- \(CS\) requests are executed in increasing order of timestamps
Requesting the Critical Section#
- When a site \(S_i\) wants to enter the CS, it broadcasts a \(REQUEST(ts_i, i)\) message to all other sites and places the request on \(request\_queue_i\).
- When site \(S_j\) receives the \(REQUEST(ts_i, i)\) message from site \(S_i\), it places site \(S_j\)'s request on \(request\_queue_j\) and returns a timestamped REPLY message to \(S_i\)
Executing the Critical Section#
Site \(S_i\) enters the CS when the following conditions hold:
- L1: \(S_i\) has received a message with timestamp larger than \((ts_i, i)\)
- L2: \(S_i\)'s request is at the top of \(request\_queue_i\)
Releasing the Critical Section#
- Site \(S_i\), upon exiting the CS, removes its request from the top of its request queue and broadcasts a timestamped RELEASE message to all other sites
- When a site \(S_j\) receives a RELEASE message from site \(S_i\), it removes \(S_i\)'s request from its request queue
Example Problem#
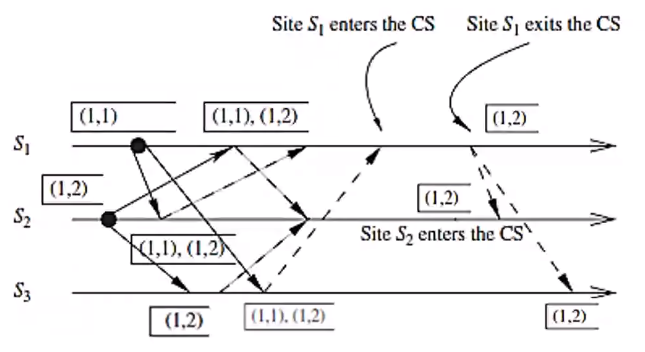
- \(S_1\) and \(S_2\) are requesting for the CS
- at \(S_2\)
- \(request\_queue_2\) \(= [(1, 2)]\)
- at \(S_1\)
- \(request\_queue_1\) \(= [(1, 1)]\)
-
\(S_1\) Receive request for CS from \(S_2\):
- \(request\_queue_1\) \(= [(1, 1),(1, 2)]\) (This priority is calculated based on the index value \(i\))
- \(S_1\) sends a REPLY to \(S_2\)
-
\(S_3\) Receive request for CS from \(S_2\):
- \(request\_queue_3\) \(= [(1, 2)]\)
- \(S_3\) sends a REPLY to \(S_2\)
- \(S_3\) Receive request for CS from \(S_1\):
- \(request\_queue_3\) \(= [(1, 1), (1, 2)]\)
- \(S_3\) sends a REPLY to \(S_1\)
- \(S_1\) enters the CS
- \(S_1\) sends RELEASE message
- \(S_2\) removes \((1,1)\) from \(request\_queue_2\)
- \(S_2\) enters the CS
- \(S_3\) removes \((1,1)\) from \(request\_queue_3\)
- \(S_2\) sends RELEASE message
- \(S_1\) removes \((1,2)\) from \(request\_queue_1\)
- \(S_3\) removes \((1,2)\) from \(request\_queue_3\)
