Week 5

Lecturer: G Venkiteswaran, Faculty for BITS Pilani

Date: 29/Aug/2021

Topics Covered

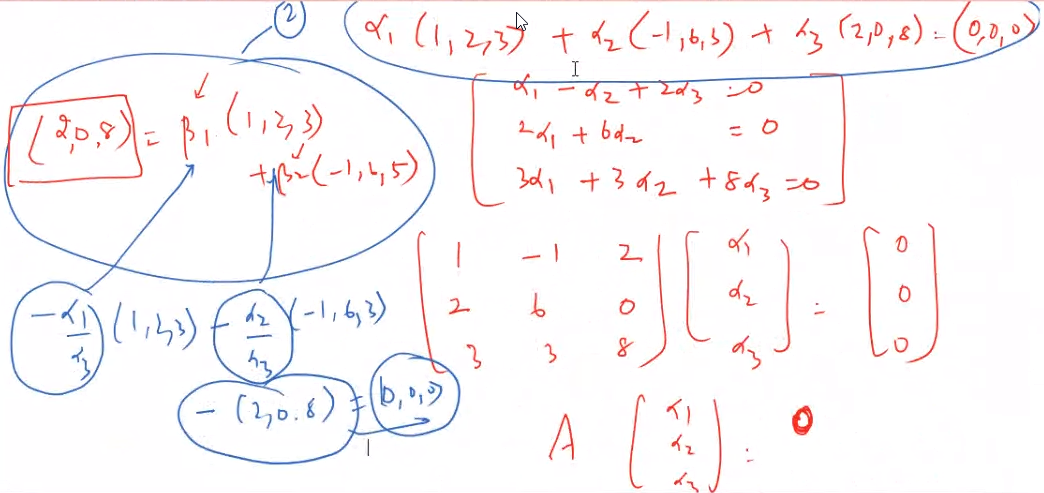
• S LI, LS(s) = V
  S is a basus No. of elements of S is dimension
• Several bases for V but dimenstion is the same
• Any set that contains 0 is LD
• Any non zero vector is LI

Construction of Basis
\(S = {v_1}\)
\(v_1 \ne 0\)
Span S =

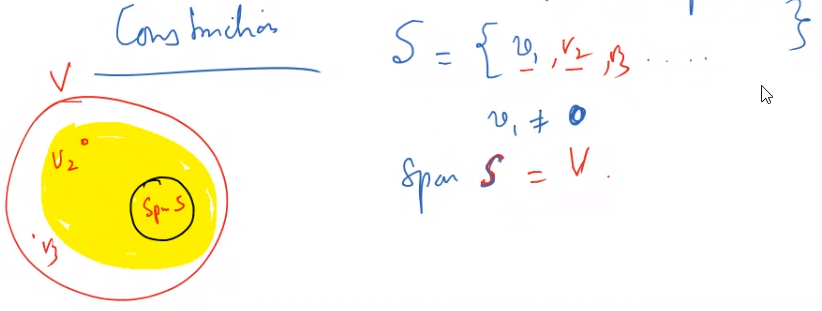
Example
Consider a 3d space of x, y, z, and a span set as:
S = {(1, 0, 0)}
We can say that this does not span the entire spce, but it does cover the x axis
Now if we take:
S = {(1, 0, 0), (0, 1, 0), (0, 0, 1)}

This set S is the Basis of

Row space and common space

Row Space

Column Space

Null Space/ Solution Space

Example

Theorem

Nullity and Rank of Matrix

Example

Linear Transformation

Range and Kernel

Rank Nullity Theorem Example

Example 1:

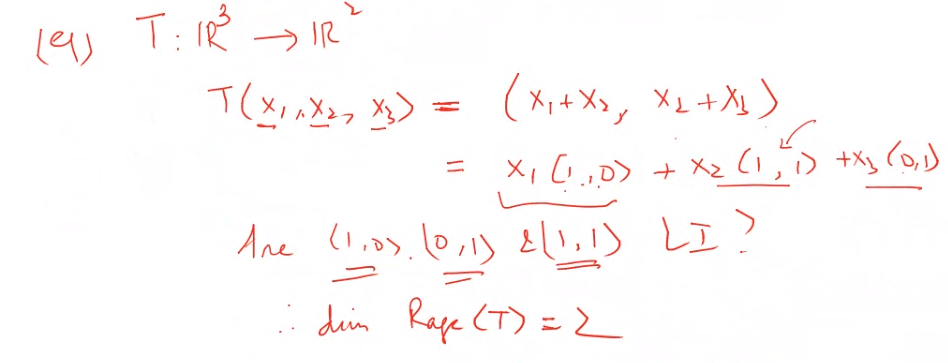
Example 2:

---

Tags: !MathematicalFoundationsIndex