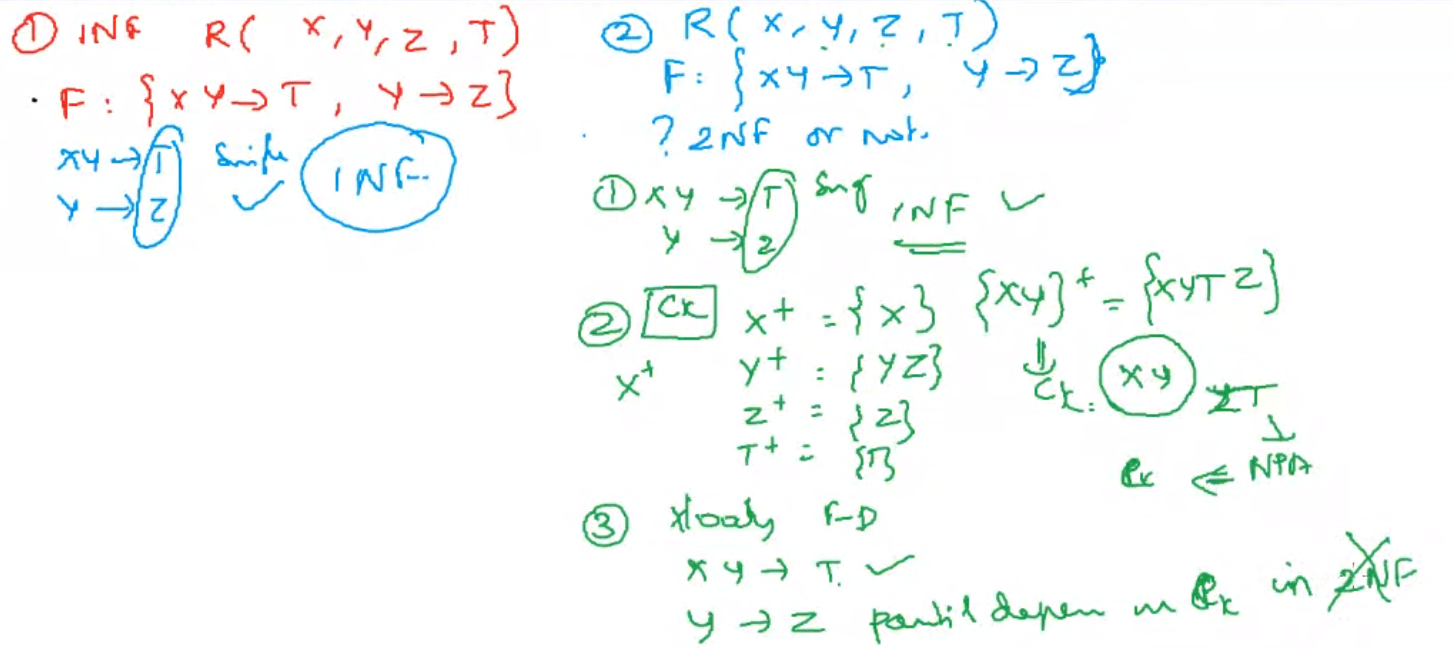Week 9

Lecturer: Uma Maheswari, Faculty for BITS Pilani WILP

Date: 16/Oct/2021

Topics Covered

Normalization or Logical Design

Functional Dependencies

Here you can see that the \(roll_no\) is a functional dependency because it can be used to get other values

Key Terms

Armstrong's axioms/properties of functional dependencies

Functional Dependency

Multivalued Functional Dependency

Trivial Functional Dependency

Non Trivial Functional Dependency

Transitive Functional Dependency

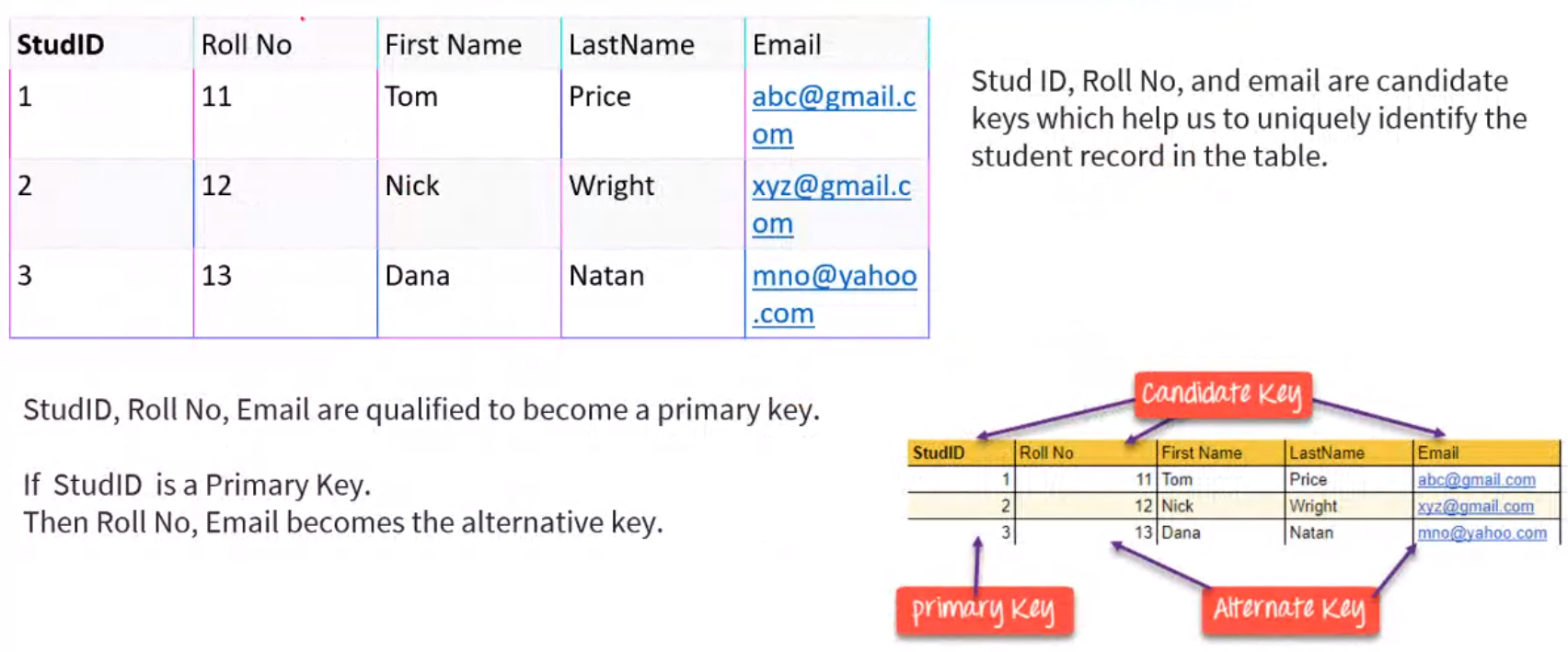
Keys

Primary Keys

Foreign Keys

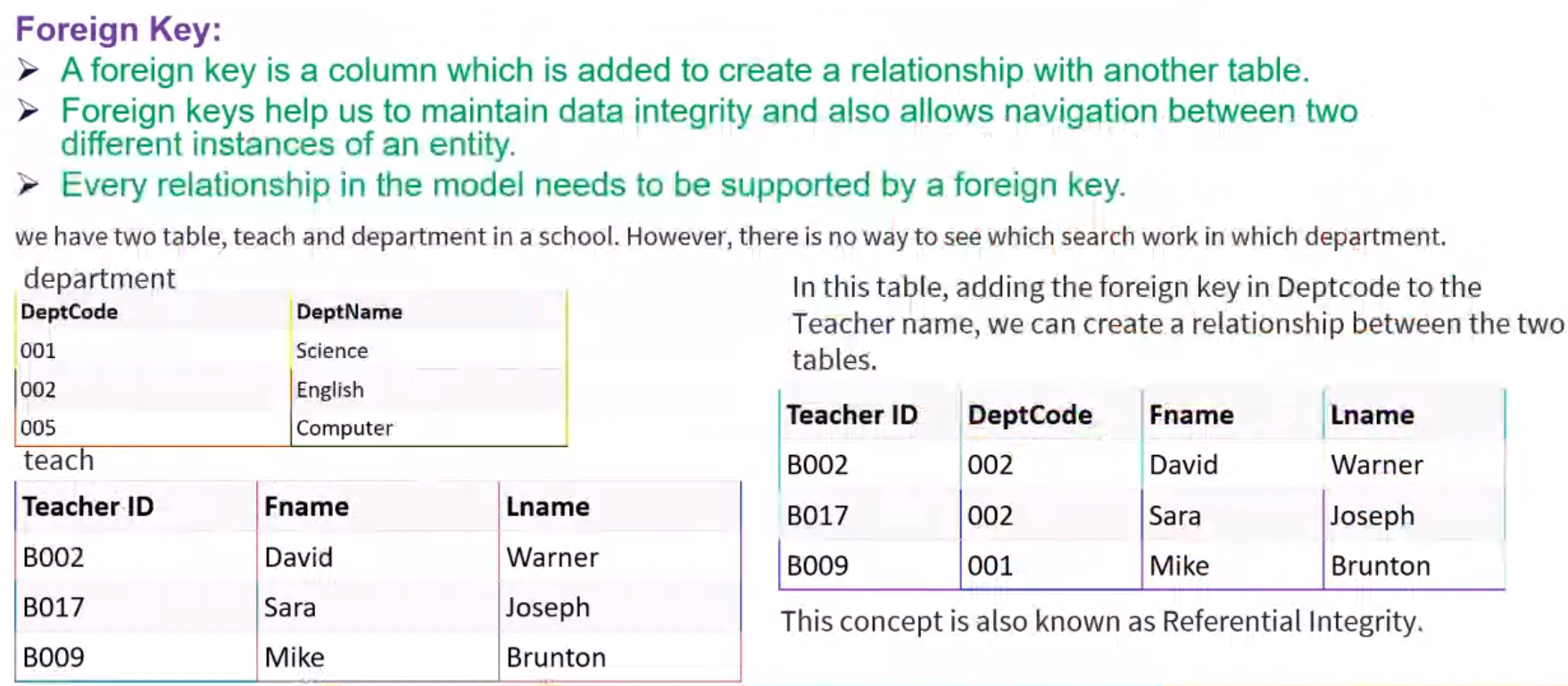
Foreign Keys help in maintaining the Referential Integrity between tables

Compound Keys

Composite Keys

Surrogate Key

The DBMS automatically creates a surrogate key

Normalization

Tutorial

Normal Forms

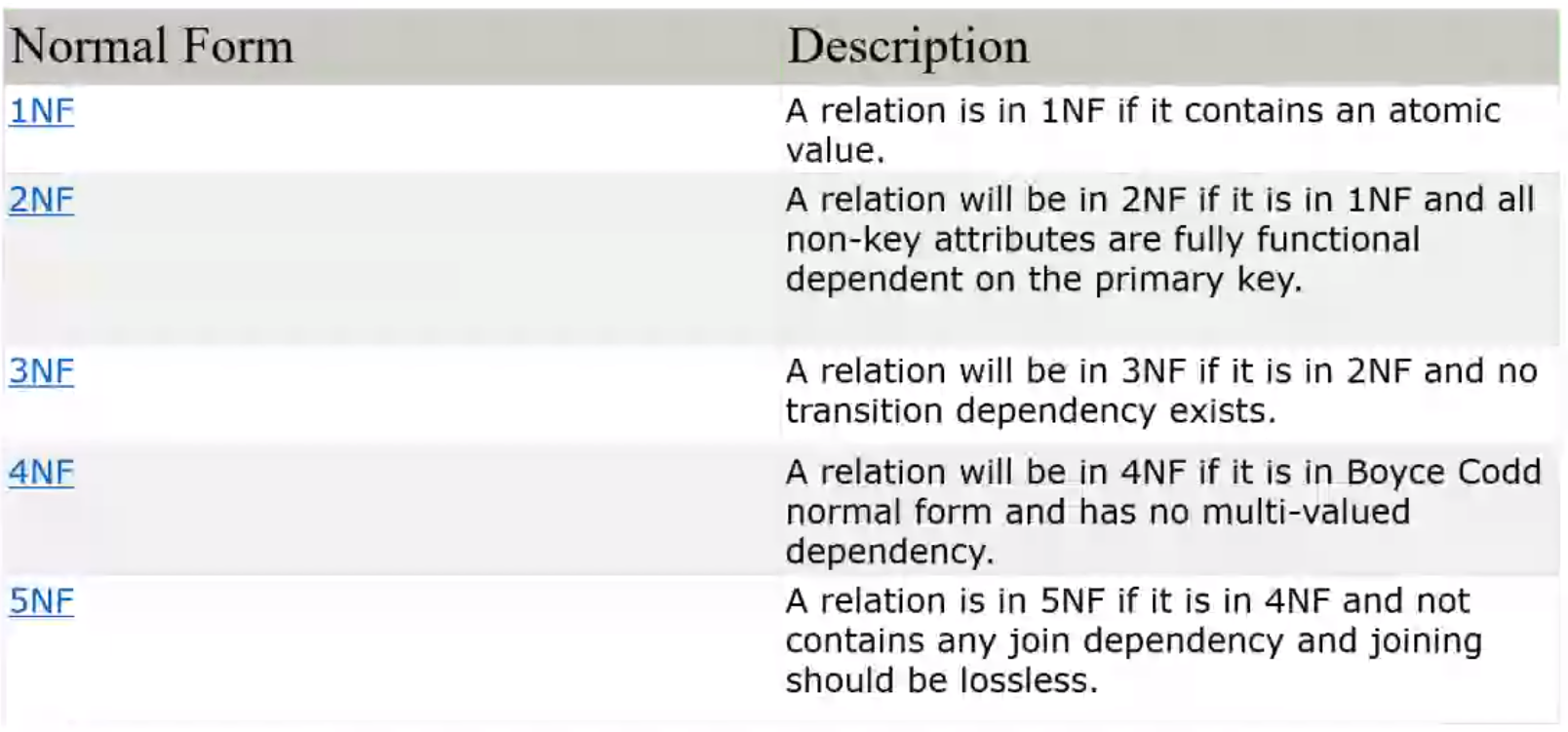
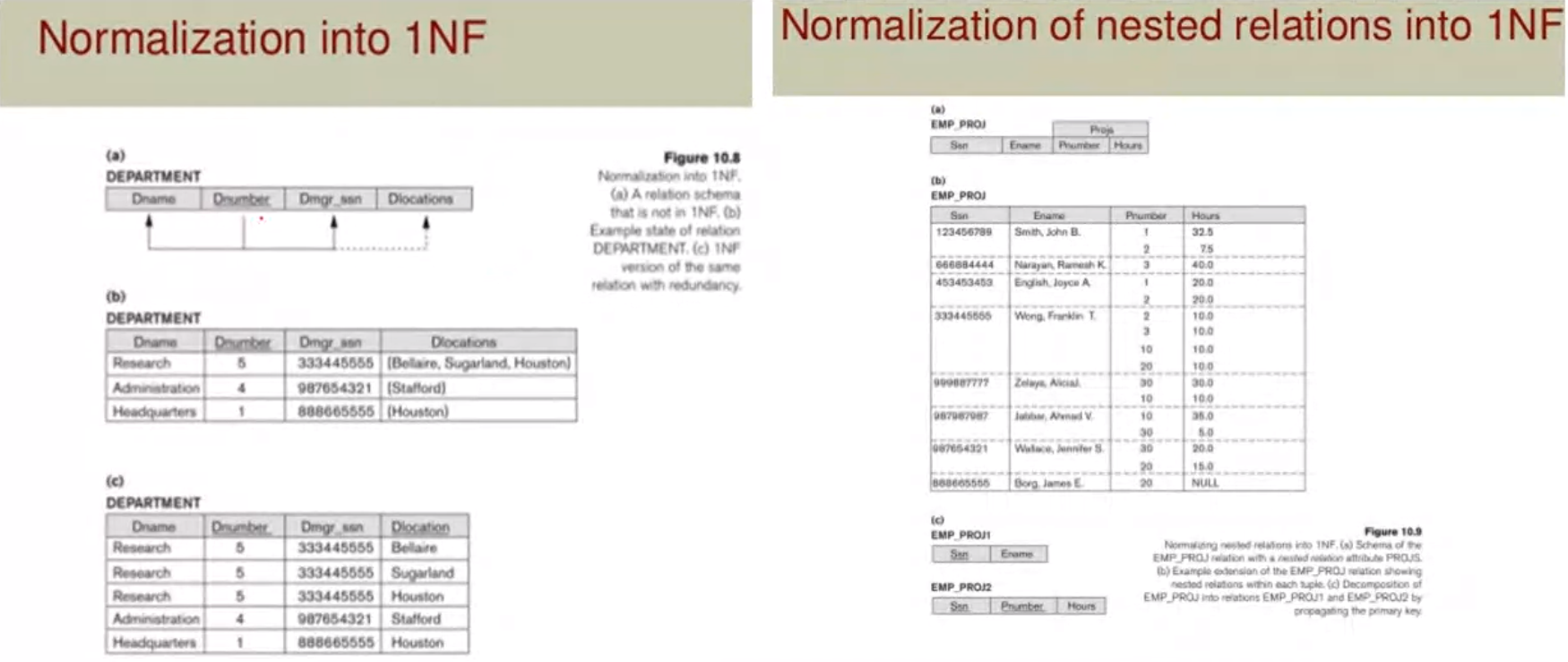
1NF

In a functional dependency if the RHS has only one attribute then it is in 1NF

Another way to do this is as follows:

Employee Details:

EMP_ID	EMP_NAME	EMP_STATE

Employee Phone Numbers:

EMP_ID	PH_NO

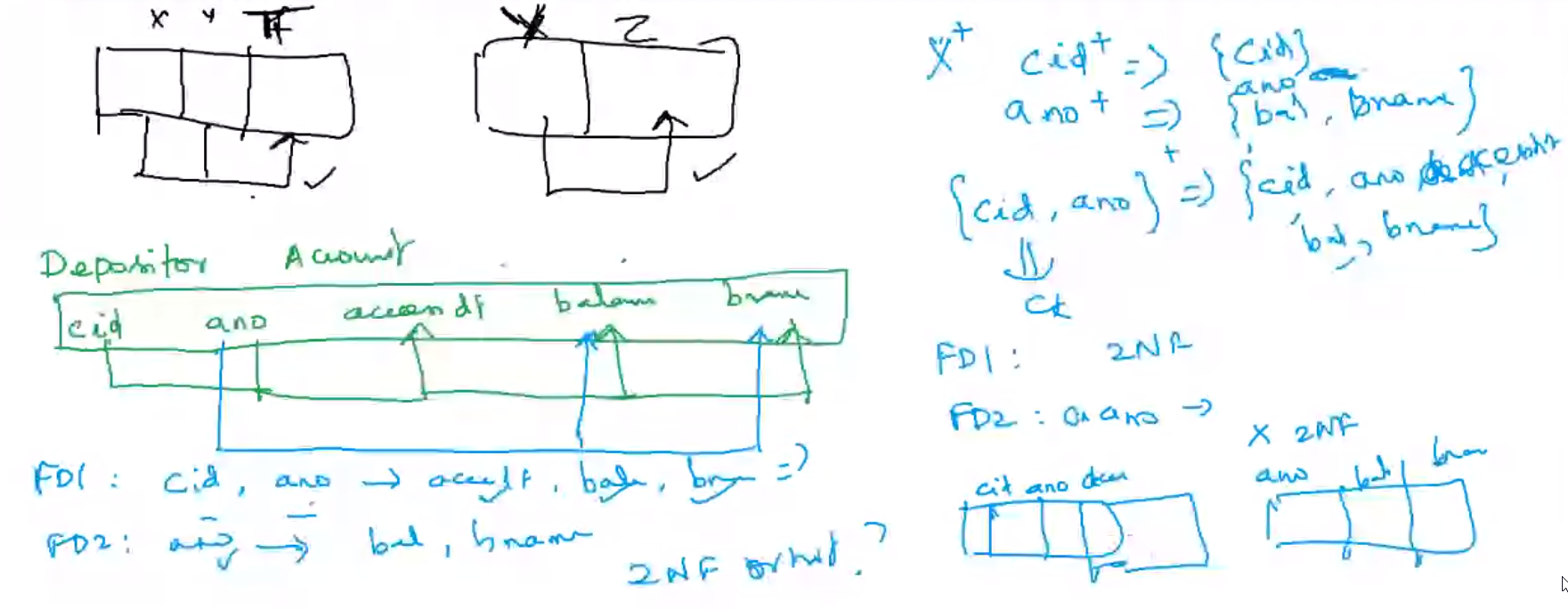
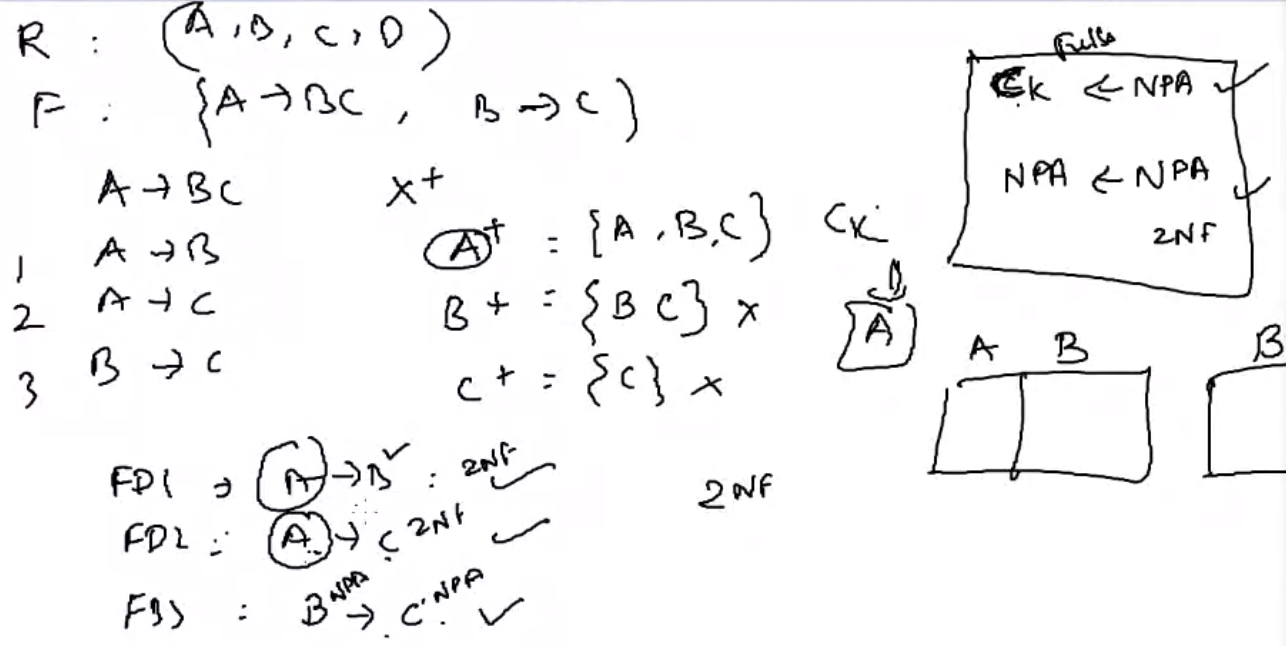
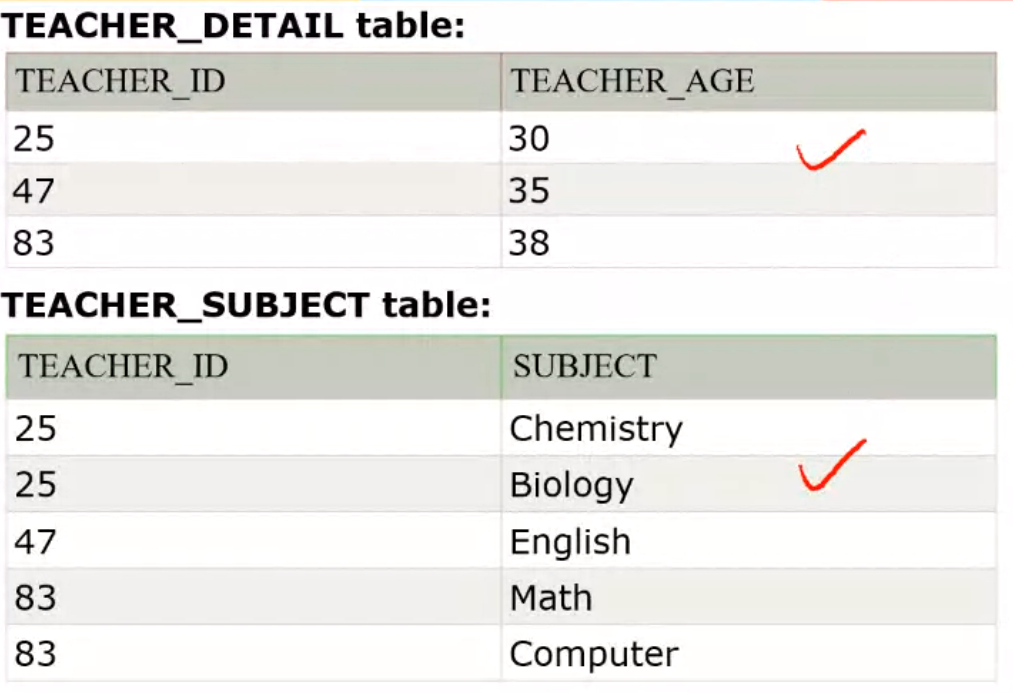
2NF

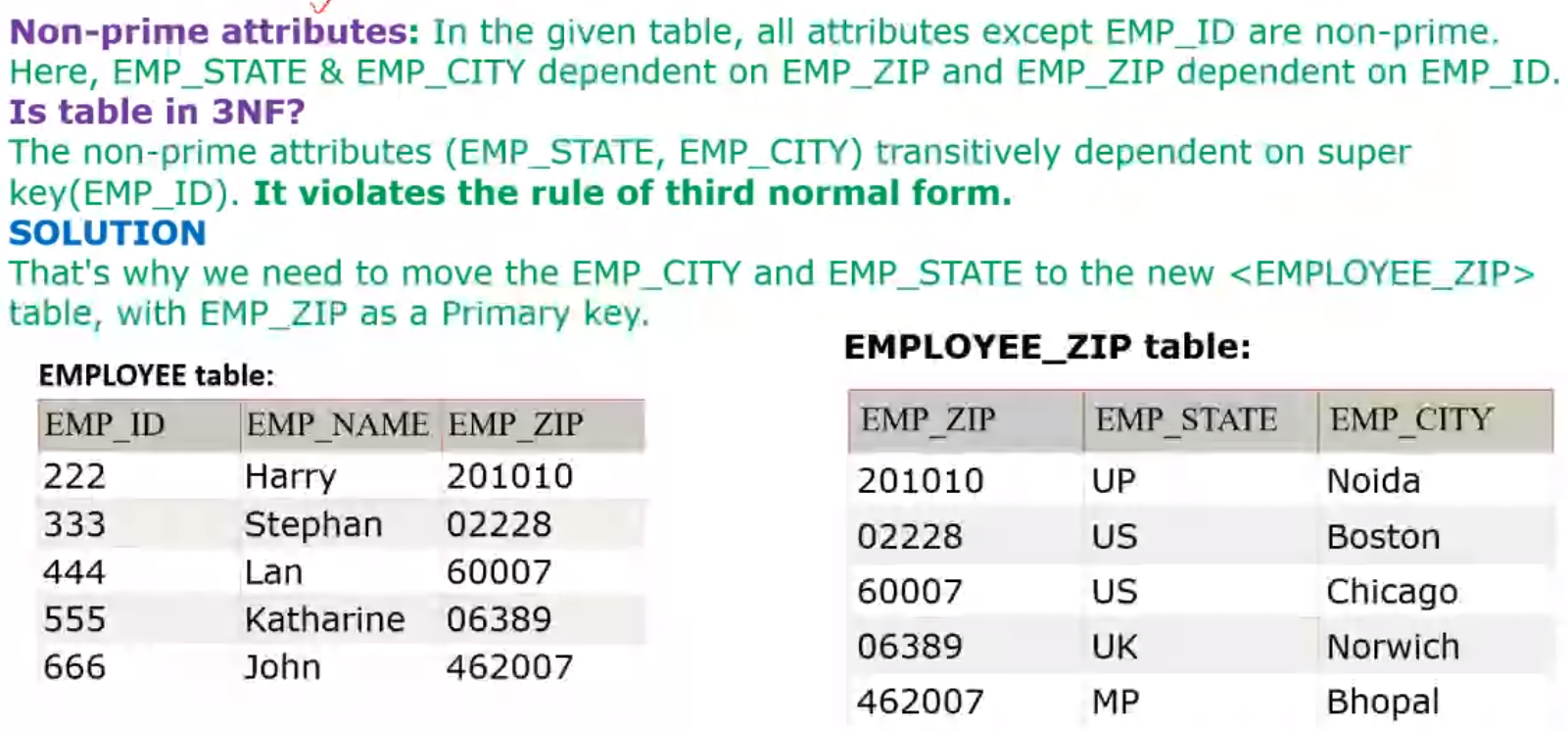
3NF

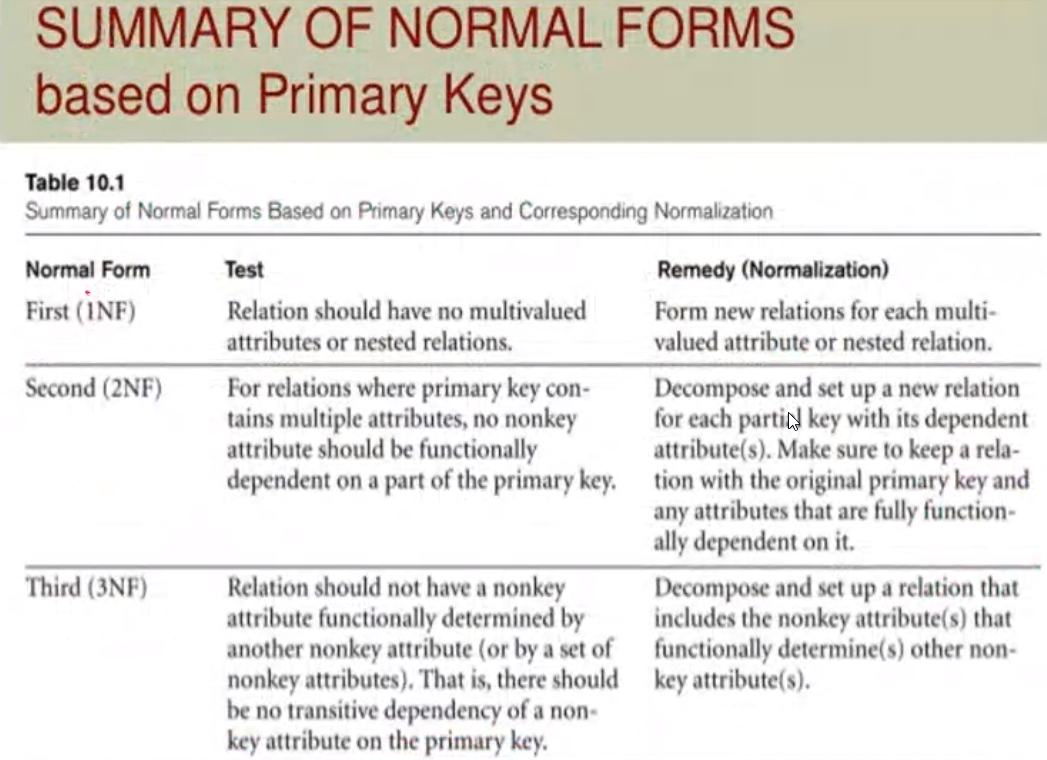
Summary of 1, 2, 3 NF

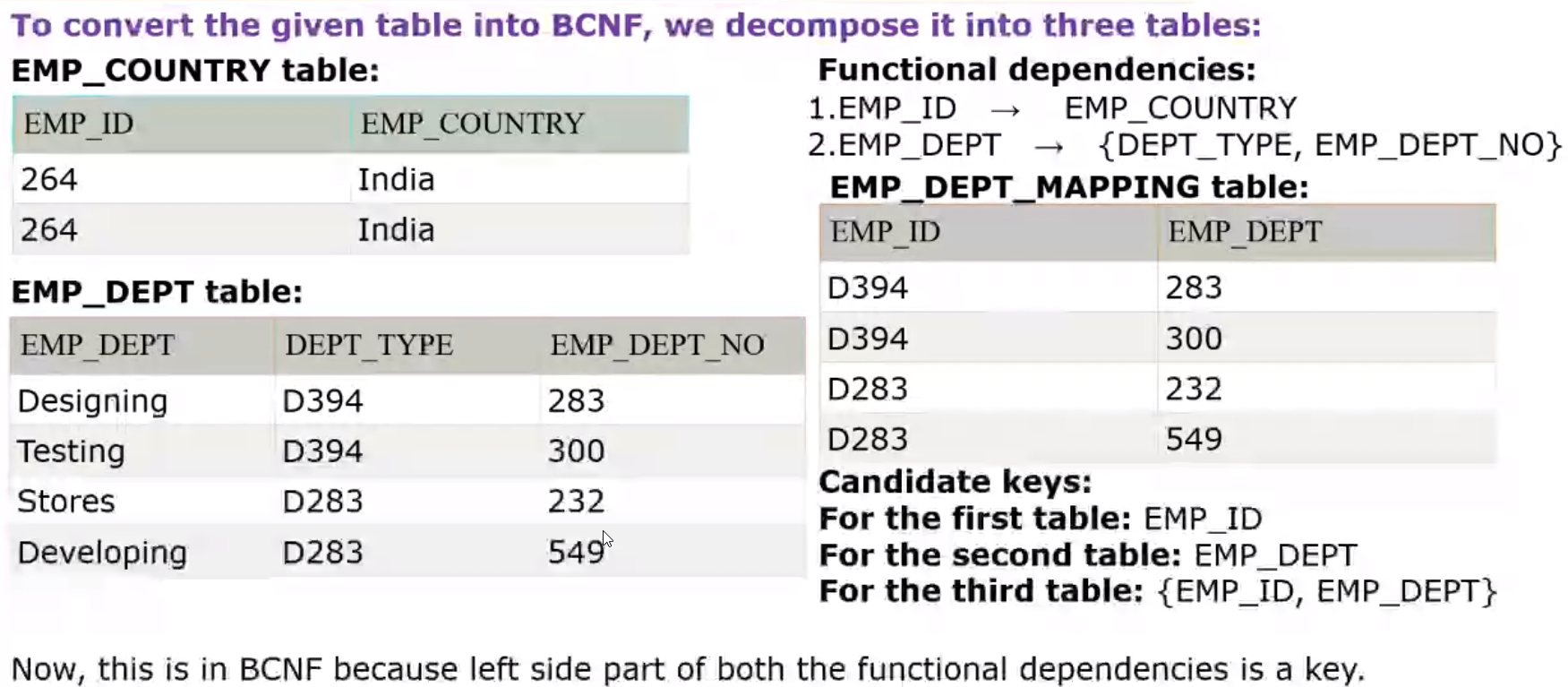
BCNF

4NF

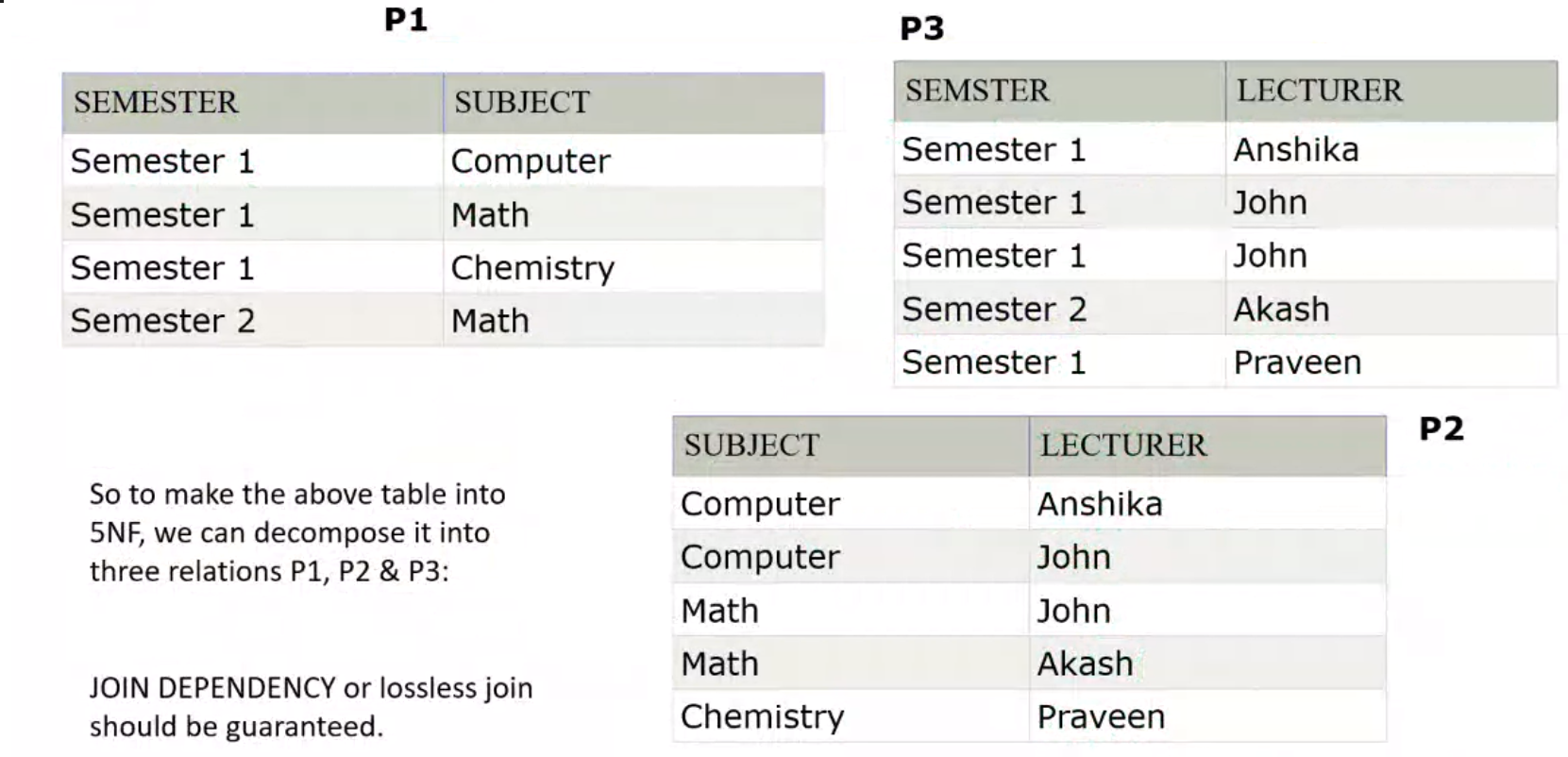
5NF

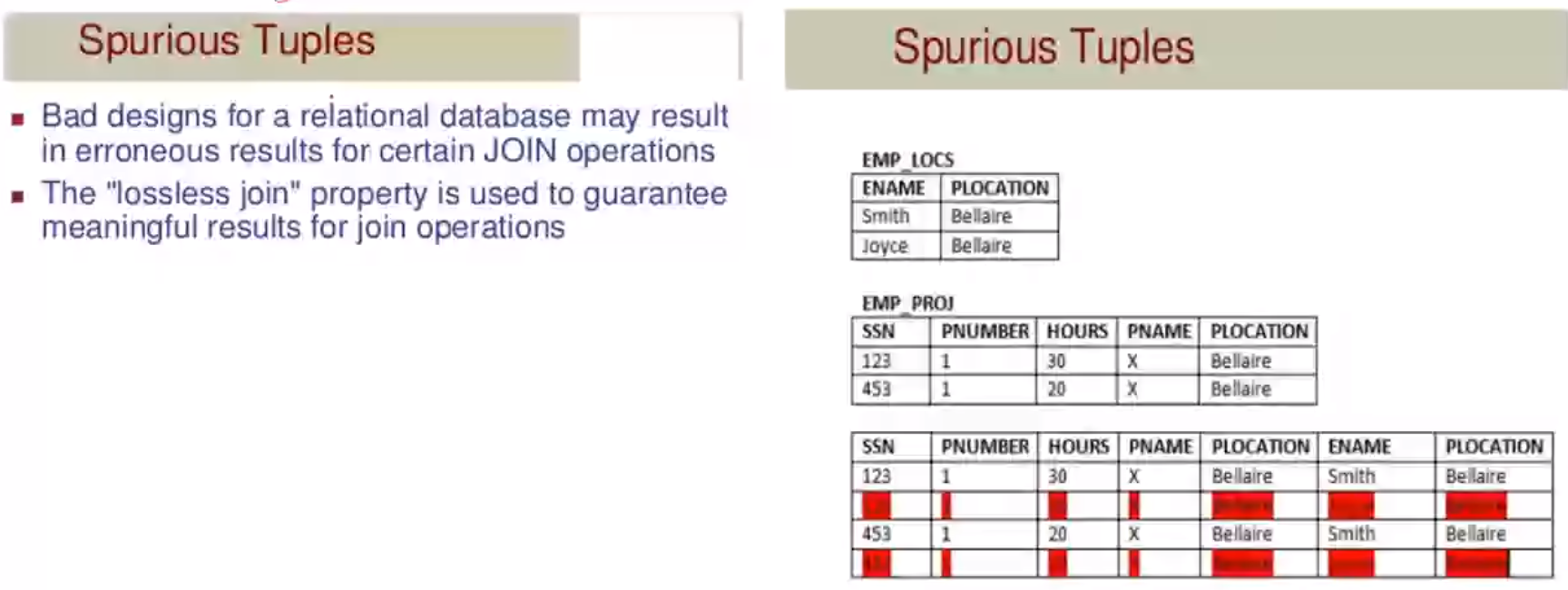
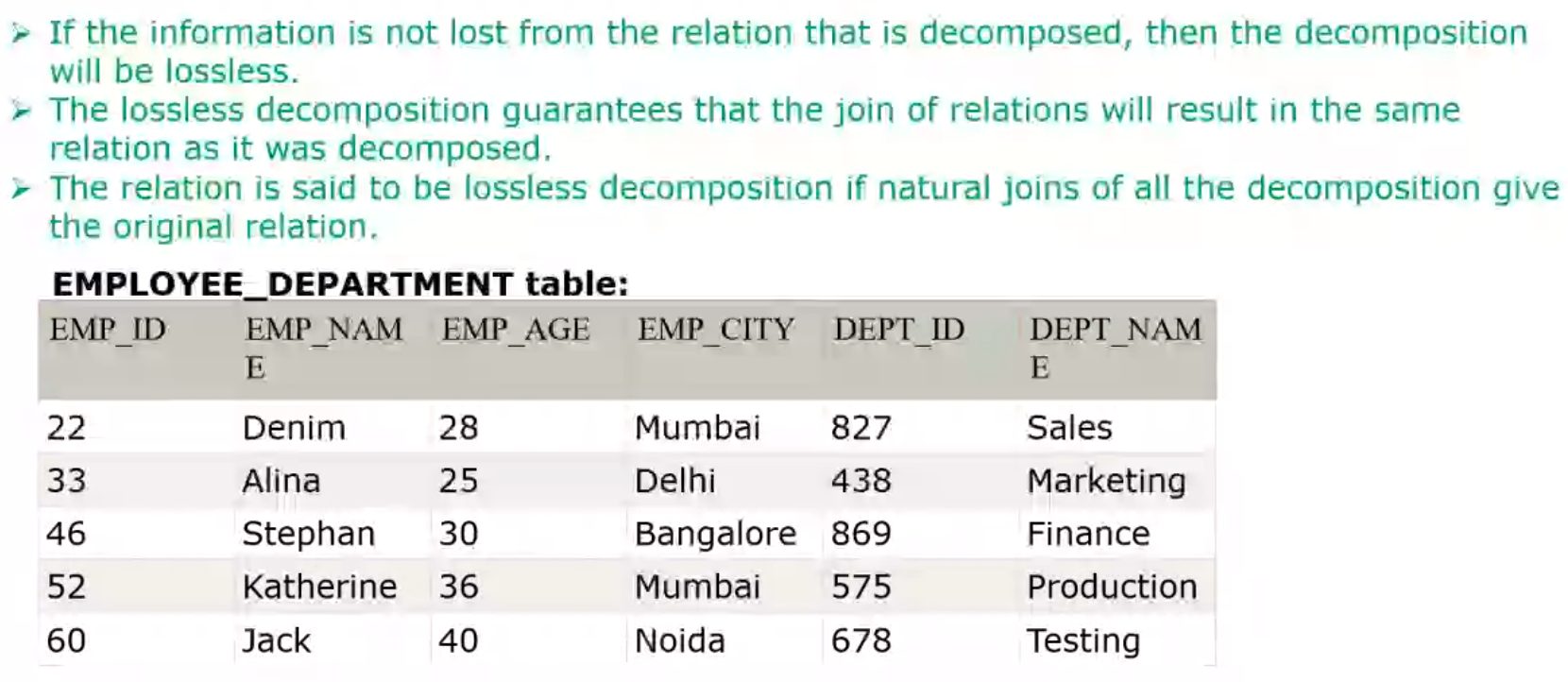
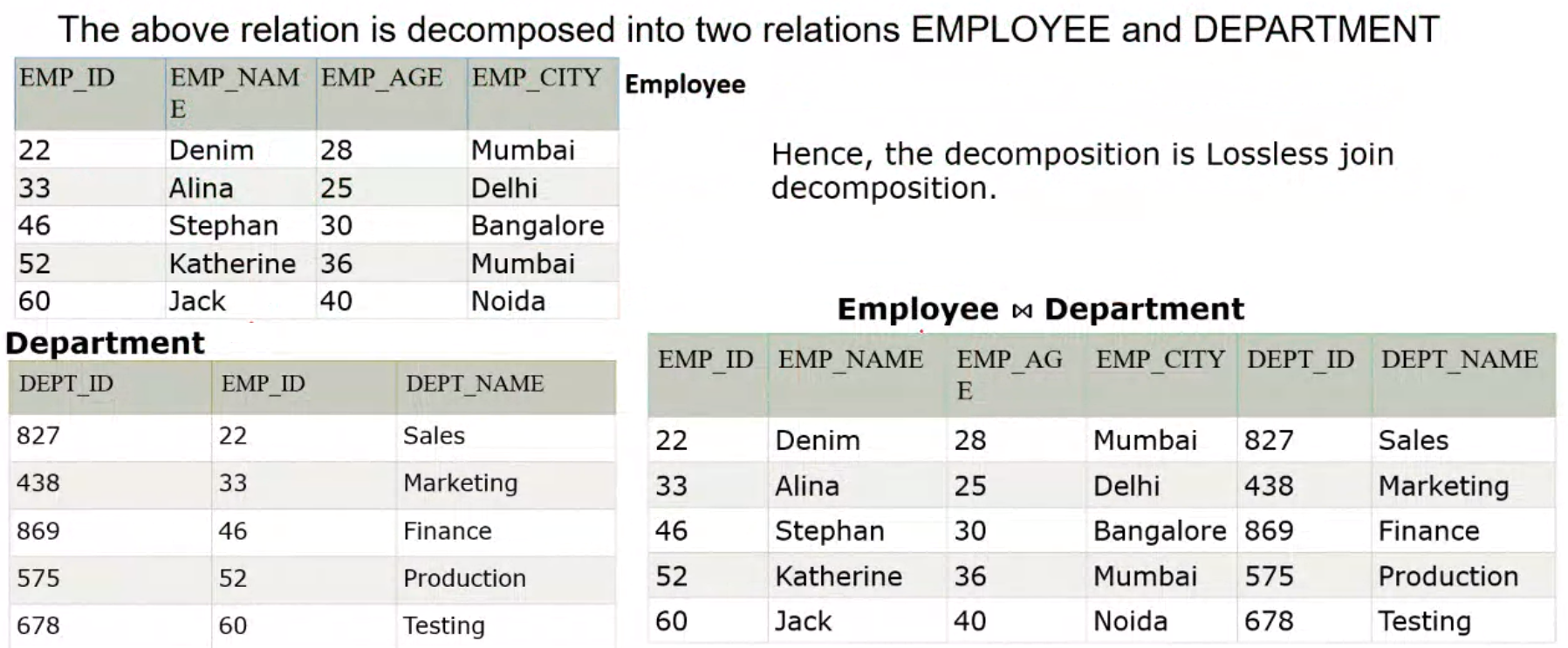
Spurious Tuples

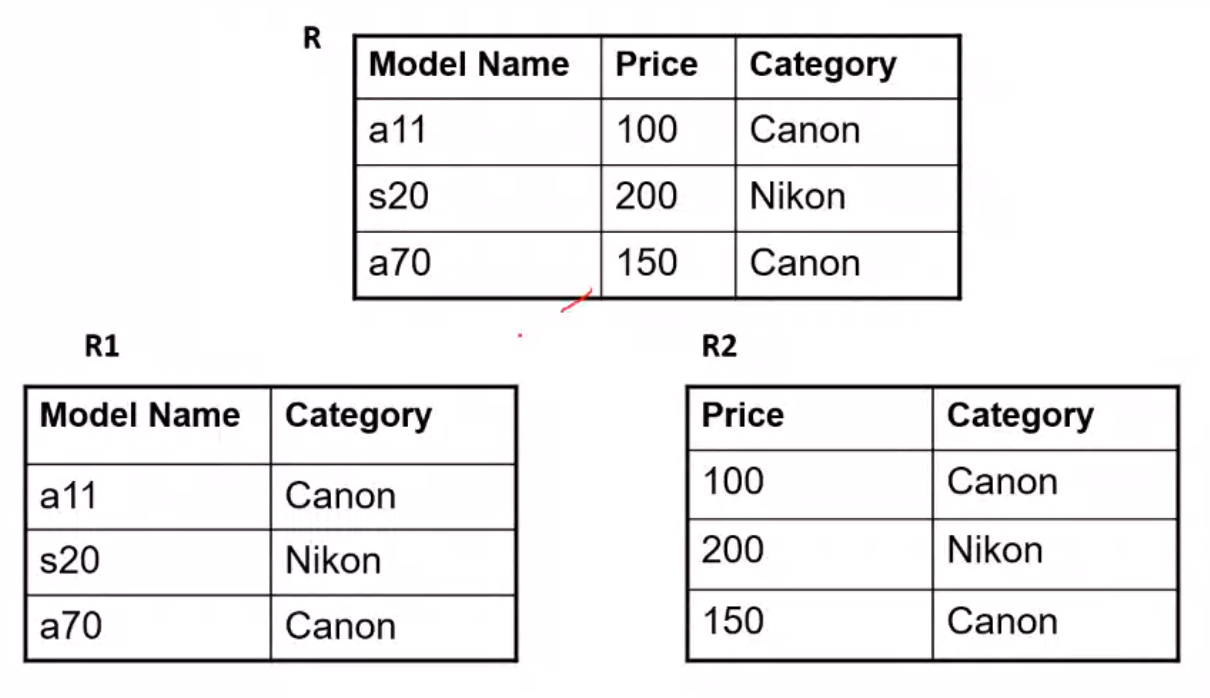
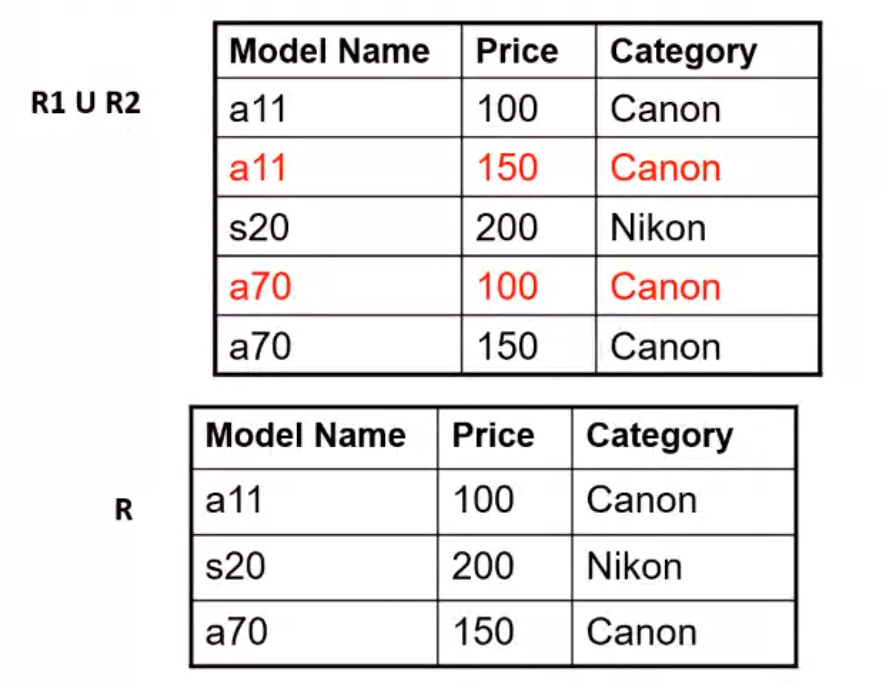
Lossless Decomposition

Extraneous Attributes

Example 1

\(R(A, B, C)\)
\(F: \{A \rightarrow B, B \rightarrow C\}\)
Since:
1. \(A^+ \implies \{A, B, C\}\), hence we can say that \(A\) is a \(CK\)
2. \(B^+ \implies \{B, C\}\), since all other attributes cannot be derived, \(B\) cannot be a \(CK\)
3. \(C^+ \implies \{C\}\), since all other attributes cannot be derived, \(C\) cannot be a \(CK\)

Example 2

\(R(A, B, C, D, E)\)
\(F: \{A \rightarrow D, BC \rightarrow A, BC \rightarrow D, C \rightarrow B, E \rightarrow A, E \rightarrow D\}\)

\(B^+ \implies \{B\}\)
\(C^+ \implies \{C, B, A, D\}\)

Since C covers all attributes we can remove the extraneous attributes from:
\(BC \rightarrow A, BC \rightarrow D\) to \(C \rightarrow A, C \rightarrow D\)

Canonical/Minimal Cover Problem

1. RHS must be singleton
2. Extraneous attributes must be resolved
3. Remove redundant FD

Example

\(R(A, B, C)\)
\(F: \{A \rightarrow B, AB \rightarrow C\}\)
1. Both relations have a singleton RHS
2. The second one has extraneous attributes
\(A^+ \implies \{ABC\}\)
\(B^+ \implies \{B\}\)
Since A covers B we can reduce the second relation to: \(A \rightarrow C\)

so the minimal cover is:
\(F: \{A \rightarrow B, A \rightarrow C\}\)

Example

\(R(A, B, C, D)\)
\(F: \{A \rightarrow B, AB \rightarrow C, D \rightarrow AC, D \rightarrow E\}\)
Does \(F\) cover \(G\)?
\(G: \{A \rightarrow BC, D \rightarrow AB\}\)

For \(F\)

1. Decomposing to singleton relations:
   \(A \rightarrow B\)
   \(AB \rightarrow C\)
   \(D \rightarrow A\)
   \(D \rightarrow C\)

2. Resolve Extraneous attributes:
   \(AB \rightarrow C\)
   \(A^+ \implies \{ABC\}\)
   \(B^+ \implies \{B\}\)

new \(F\):
\(\{A \rightarrow B, A \rightarrow C, D \rightarrow A, D \rightarrow C, D \rightarrow E\}\)

1. Redundant FD
   Since the dependency \(D \rightarrow C\) is not needed we can drop that dependency

Final \(F\):
\(\{A \rightarrow B, A \rightarrow C, D \rightarrow A, D \rightarrow E\}\)

For \(G\)

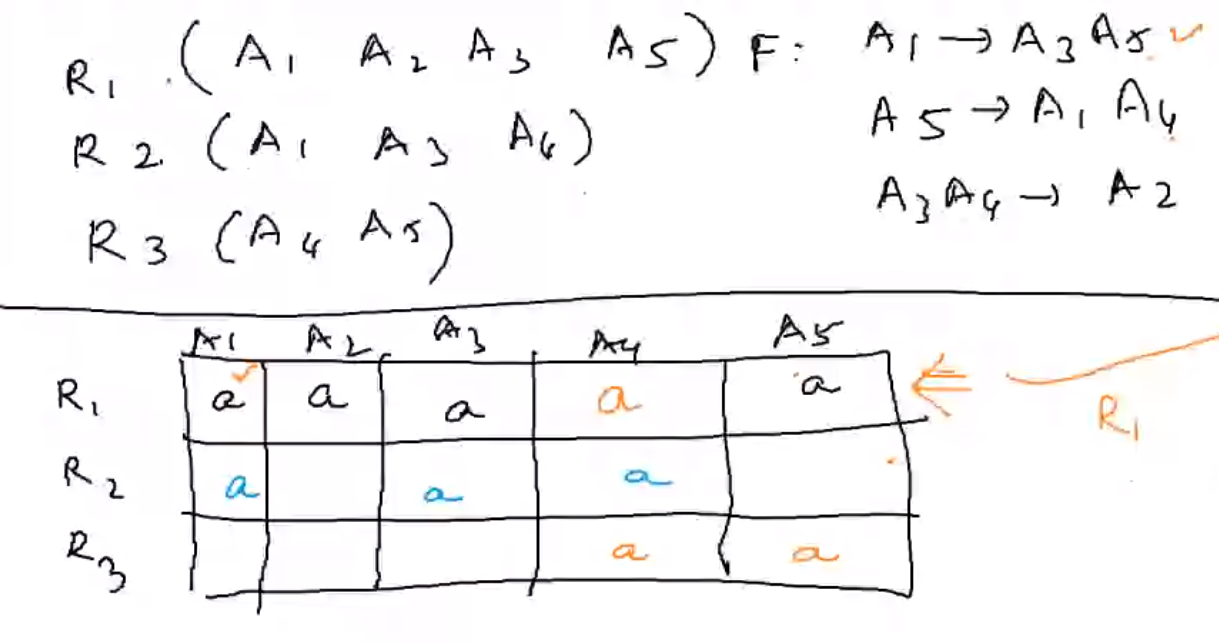
Normalization Problems

---

Tags: !DatabaseDesignAndApplicationIndex