Week 4#
Lecturer: Pritam Bhattacharya, BITS Pilani, Goa Campus
Date: 21/Aug/2021
Topics Covered#
- Deriving Big\(\mathcal{O}\) From Growth Rate
- Significance of Growth Rate
- Examples
- Rules to Find Big\(\mathcal{O}\) Notation
Deriving Big\(\mathcal{O}\) From Growth Rate#
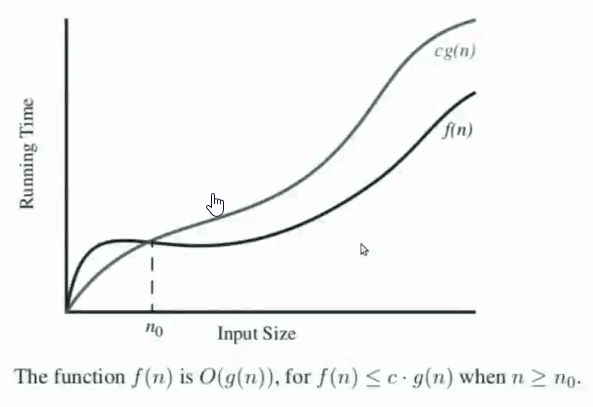
Significance of Growth Rate#
Consider f(n) and g(n), Let us consider what a growth rate of a function is.
Growth rate
\(f(n) = 1000n\)
\(g(n) = 2n^2\)
| \(n\) | \(f(n)\) | \(g(n)\) | \(f(n)/f(n-1)\) | \(g(n)/g(n-1)\) |
|---|---|---|---|---|
| 1 | 1000 | 2 | - | - |
| 2 | 2000 | 8 | 2 | 4 |
| 3 | 3000 | 18 | 1.5 | 2.25 |
| 4 | 4000 | 32 | 1.33 | 1.78 |
| 5 | 5000 | 50 | 1.2 | 1.56 |
Seeing the above pattern in the rate of growth, we see that for any particular value of \(n\) the \(g(n)\) ratio is bigger than that for \(f(n)\), and this is seen as we incrementing \(n\). So we can conclude that \(g(n)\) has a faster rate of growth.
We can also find the value of n for which the value of \(g(n)\) will shoot up more than \(f(n)\):
\(g(n) \ge f(n)\)
\(2.n^2 \ge 1000n\)
\(n \ge 500\)
This shows that since the \(g(n)\) grows faster (quadratic growth), whenever \(n\) is greater than \(500\) then \(g(n)\) will always be greater than \(f(n)\) so we can conclude that the algorithm that has a run time of \(f(n)\) will be overall better than one that has a run time of \(g(n)\).
Examples#
Example 1: \(f(n) = 20.n^3 + 10.n.log(n) + 5\) is \(\mathcal{O}(n^3)\)
Proof: \(20.n^3 + 10.n.log(n) + 5 \le 35.n^3\), for \(n \ge 1\)
Example 2: \(f(n) = 2^{100}\) is \(\mathcal{O}(1)\)
Proof: \(2^{100} \le 2^{100}.1\), for \(n \ge 1\)
Example 3: \(f(n) = 3^log(n) + log(log(n))\) is \(\mathcal{O}(log(n))\)
Proof: \(3^log(n) + log(log(n)) \le log(n)\), for \(n \ge 2\) and \(c = 4\)
Rules to Find Big\(\mathcal{O}\) Notation#
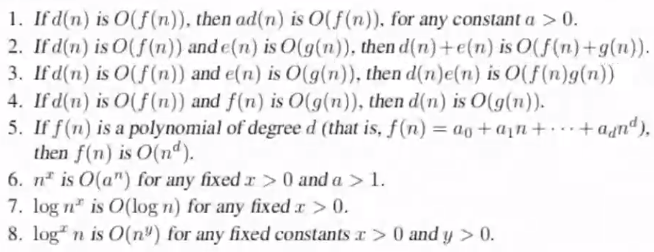
Some examples:

