Week 3#
Lecturer: Barsha Mitra, BITS Pilani, Hyderabad Campus
Date: 07/Aug/2021
Topics Covered#
- Models of Communication Networks
- FIFO Model
- Non FIFO Model
- Causal Ordering Model
- Global State of a DS
- Consistent Global State
- Cuts of a DC
- Consistent vs inconsistent cut
- Logical Time
- Scalar Time
- Notations
- Rules for updating scalar clock
- Height of an event
- Vector Time
- Notations
- Rules for updating vector clock
- Event Counting
- Scalar Time
Models of Communication Networks#
FIFO Model#
- Each channel acts as a FIFO queue
- Since the messages are sent in a queue, ordering is preserved by the channel
- If \(P_1\) sends \(m_1\), \(m_2\) to \(P_2\) then \(P_2\) receives those two messages as a queue in the same order
Non FIFO Model#
- The channel acts as a set of messages
- Since it is a set, the messages do not necessarily have the order maintained
- Sender process adds messages to channel
- Receiver process removes messages from it
- This helps in relieving the communication network from the overhead of maintaining the message ordering
Causal Ordering Model#
- This is based on the happens before relation.
- Such a system must satisfy:
- If there are two messages \(m_{ij}\) and \(m_{kj}\), then if \(Send(m_{ij}) \rightarrow Send(m_{kj})\), then it must also follow \(Rec(m_{ij}) \rightarrow Rec(m_{kj})\)
- Note that the messages are coming to the same process.
- Causally ordered messages implies FIFO message delivery
- \(CO \subset FIFO \subset Non FIFO\)
Global State of a DS#
More details here Week2DC#Notations.
- \(LS_i^x\) : State of process \(p_i\) after the occurrence of event \(e_i^x\) and before \(e_i^{x+1}\)
- \(SC_{ij}\) : State of channel \(C_{ij}\)
Consistent Global State#
- A state is meaningful, meaning that every message that is recorded as received is also recorded as sent
- For all \(m_{ij}\), \(send(m_{ij}) \notin LS_i^x\) \(\implies\) \(m_{ij} /notin SC_{ij} rec(m_{ij}) \notin LS_j^y\)
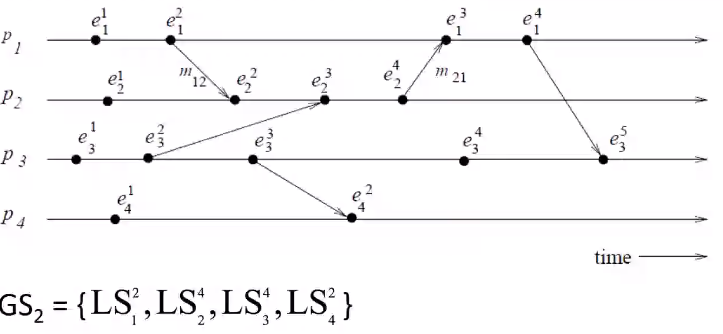
- The above space time diagram is consistent, because when we see all the \(LS\) that define the \(GS\) all the sends are recorded before the receives of that message
- Consider a \(GS\) of \(LS_1^3, LS_2^3, LS_3^4, LS_4^2\), here the \(GS\) is inconsistent, because the receive of message \(m_{21}\) is recorded but not the send.
Cuts of a DC#
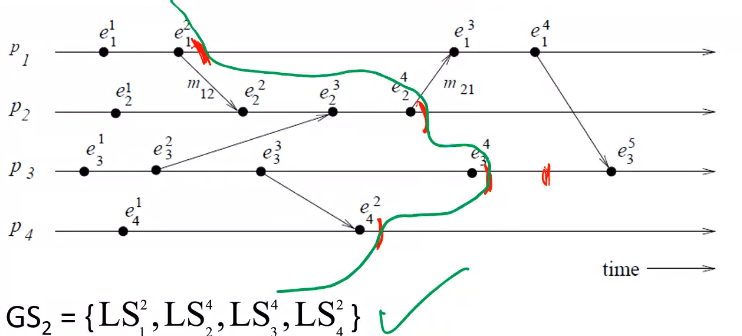
- Any zig-zag line drawn that cuts all the processes in a space time diagram
- The events in a DS is partitioned into:
- Past: Contains all events left of the cut
- Future: Contains all events right of the cut
- A cut is a representation of the \(GS\) at those points in the cut and processes
Consistent vs inconsistent cut#
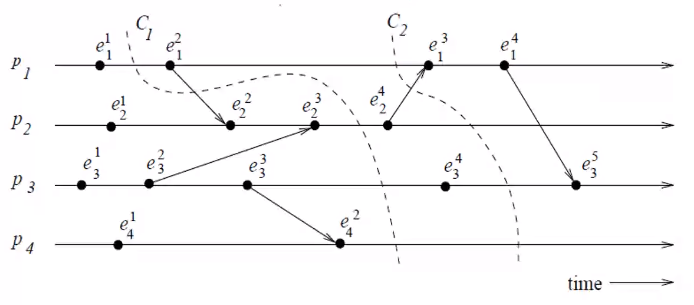
- Consistent cut:
- Every message received in the PAST of the cut was sent in the PAST of that cut
- All messages that cross the cut from the PAST to the FUTURE are in transit
- The above image \(C2\) is an example since all the sends and receives happen in the PAST and the message between \(e_2^4\) to \(e_1^3\) is in transit.
- Inconsistent cut:
- If the receive is recorded in the PAST and the send is in the FUTURE then it is an inconsistent cut
- In the above image \(C1\) is inconsistent since \(send(e_1^2)\) is in the FUTURE and \(rec(e_2^2)\) is in the past.
Logical Time#
- To show a sense of time in the sense of
- Logical time follows Monotonicity property: if event \(\alpha\) has happened before event \(\beta\) then the timestamp of event \(\alpha\) is less that the timestamp of event \(\beta\)
- Every process has a LC
- LC is advanced using a set of rules
- each event is assigned as timestamp
- There are two ways to represent logical time:
- Scalar Time
- Vector Time
Scalar Time#
Notations#
- This is covered in the pre reading content here: PreRecordedModule12#Scalar Time
- Time domain is the set of non negative integers
- \(C_i\) : Integer variable, denotes the logical clock of \(p_i\)
Rules for updating scalar clock#
-
R1: Before executing an event, process \(p_i\) executes
- \(C_i = C_i + d\ (d \gt 0)\)
- d can be any value but usually is 1
-
R2: When process \(p_i\) receives a message with a timestamp \(C_{msg}\), it executes the following actions:
- \(C_i = mac(C_i, C_{msg})\)
- execute R1
- deliver the message
- Whenever there is an internal event the R1 is executed
- The above rules can be seen in action in the steps below:
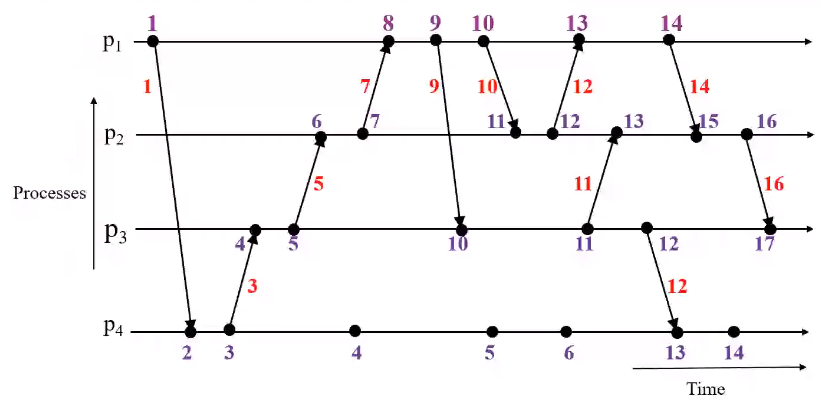
Height of an event#
- Height is defined as the number of events that causally precedes it
- If \(d = 1\), the height of a given event is 1 minus the timestamp at that event.
Vector Time#
Notations#
- Time domain is represented by a set of n-dimensional non-negative integer vectors. (Can be a row or a column vector)
- \(vt_i[i]\), \(vtj[j]\)
Rules for updating vector clock#
- R1: First take the element wise max of the vector received and the local vector
- R2: Add 1 to the local clock index of the vector decided above
- The above rules can be seen in action in the steps below:
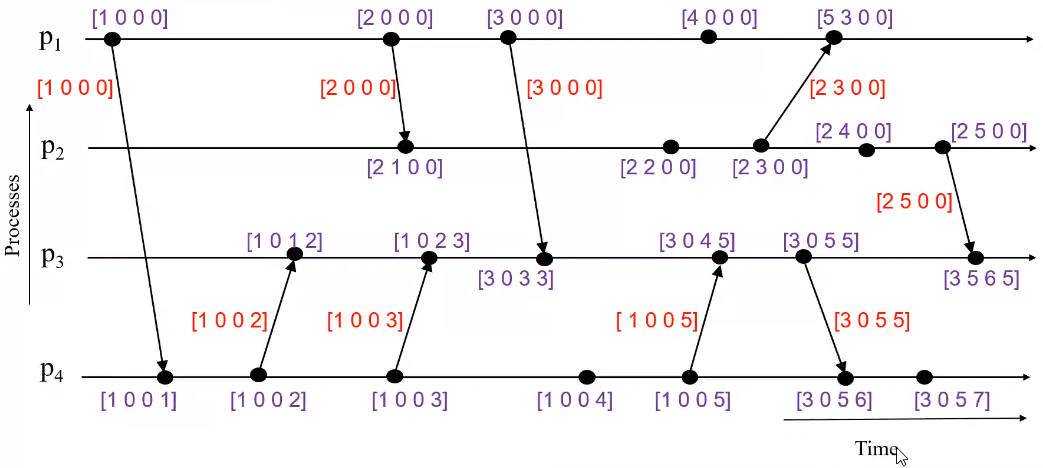
Event Counting#
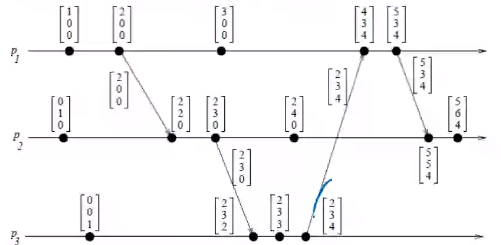
- if \(d\) is always \(1\) and \(vt_i[i]\) is the \(i^{th}\) component of vector clock at process \(p_i\)
- Then \(vt_i[i]\) = no. of events that have occurred at \(p_i\) until that instant
- \(vh[j]\) = number of events executed by process \(p_j\) that causally precede \(e\)
- \(\sum vh[j] - 1\): Total no. of events that causally precede \(e\) in the DC
