Week 6

Lecturer: Barsha Mitra, BITS Pilani, Hyderabad Campus

Date: 4/Sep/2021

Topics Covered

1. Distributed Mutual Exclusion (Cont.)
   1. Ricart Agrawala Algorithm
      1. Requesting the critical section
      2. Executing the critical section
      3. Releasing the critical section
      4. Example Problem
   2. Maekawa's Algorithm
      1. Problem Example
      2. Algorithm Steps
      3. Deadlocks
   3. Raymond's Tree Based Algorithm
      1. Example
      2. Data Structures
      3. Steps of algorithm
   4. Suzuki-Kasami's Broadcast Algorithm

Distributed Mutual Exclusion (Cont.)

Ricart Agrawala Algorithm

• Communication channels are not required to be FIFO
• \(REQUEST\) and \(REPLY\) messages
• Each process \(p_i\) maintains the request deferred array \(RD_i\)
• Size of \(RD_i\) = no. of processes in the system
• Initially, \(\forall i\ \forall j: RD_i[j] = 0\)
• Whenever \(p_i\) defers the request sent by \(p_j\), it sets \(RD_i[j] = 1\)
• After it has sent a \(REPLY\) message to \(p_j\), it sets \(RD_i[j] = 0\)

Requesting the critical section

• When a site \(S_i\) wants to enter the CS, it broadcasts a timestamped \(REQUEST\) message to all other sites
• When site \(S_j\) receives a \(REQUEST\) message from site \(S_i\), it sends a \(REPLY\) message to site \(S_i\) if site \(S_j\) is neither requesting nor executing the CS, or if the site \(S_j\) is requesting and \(S_i\)'s request's timestamp is smaller than site \(S_j\)'s own requests's timestamp. Otherwise, the reply is deferred and \(S_j\) sets \(RD_j[i] = 1\)

Executing the critical section

Site \(S_i\) enters the CS after it has received a \(REPLY\) message from every site it sent a \(REQUEST\) message to

Releasing the critical section

When site \(S_i\) exits the CS, it sends all the deferred REPLY messages:
\(\forall\ j\) if \(RD_i[j] = 1\), then \(S_i\) sends a REPLY message to \(S_j\) and sets \(RD_i[j] = 0\)

Example Problem

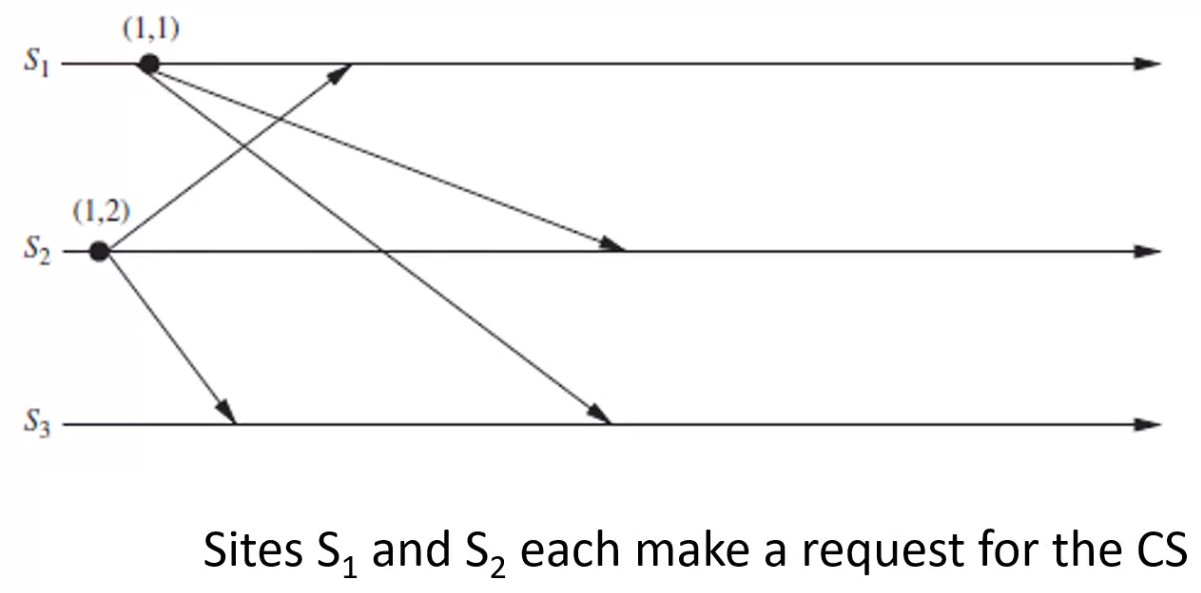
- \(S_1\) has timestamp \((1, 1)\)
- \(S_2\) has timestamp \((1, 2)\)

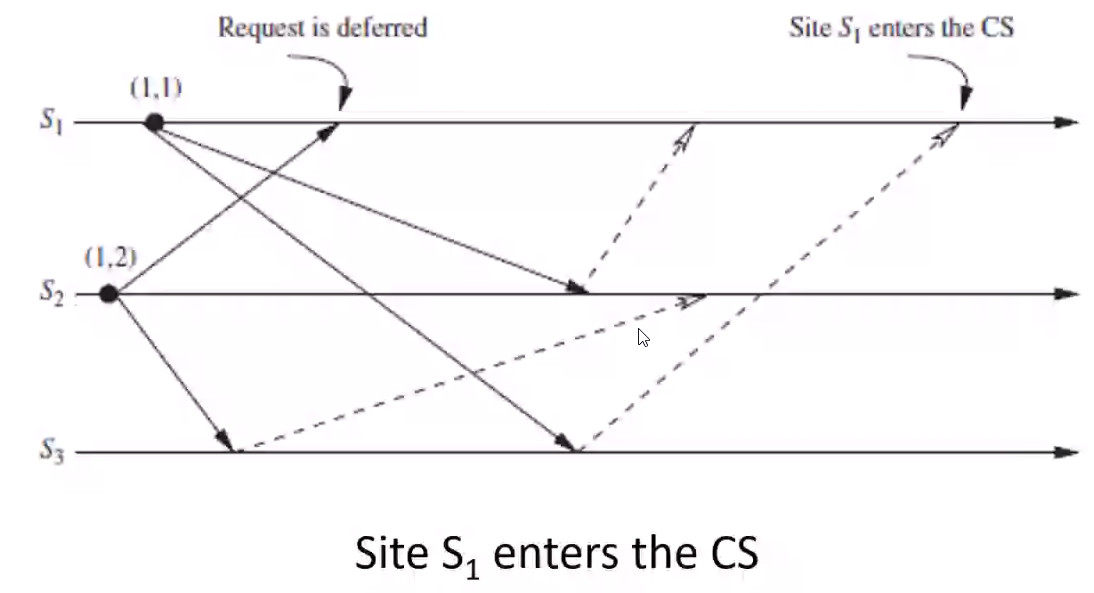
- \(S_3\) receives \(S_2\) request so sends \(REPLY\) (dotted line) to \(S_2\)
- \(S_1\) defers \(S_2\) request since it needs to get CS
- \(S_2\) sends \(S_1\) \(REPLY\) since \(S_1\) has higher priority
- \(S_3\) sends \(S_1\) \(REPLY\)
- \(S_1\) enters CS since it received \(REPLY\) from all other sites
- At this point \(RD_1 = [0, 1, 0]\)

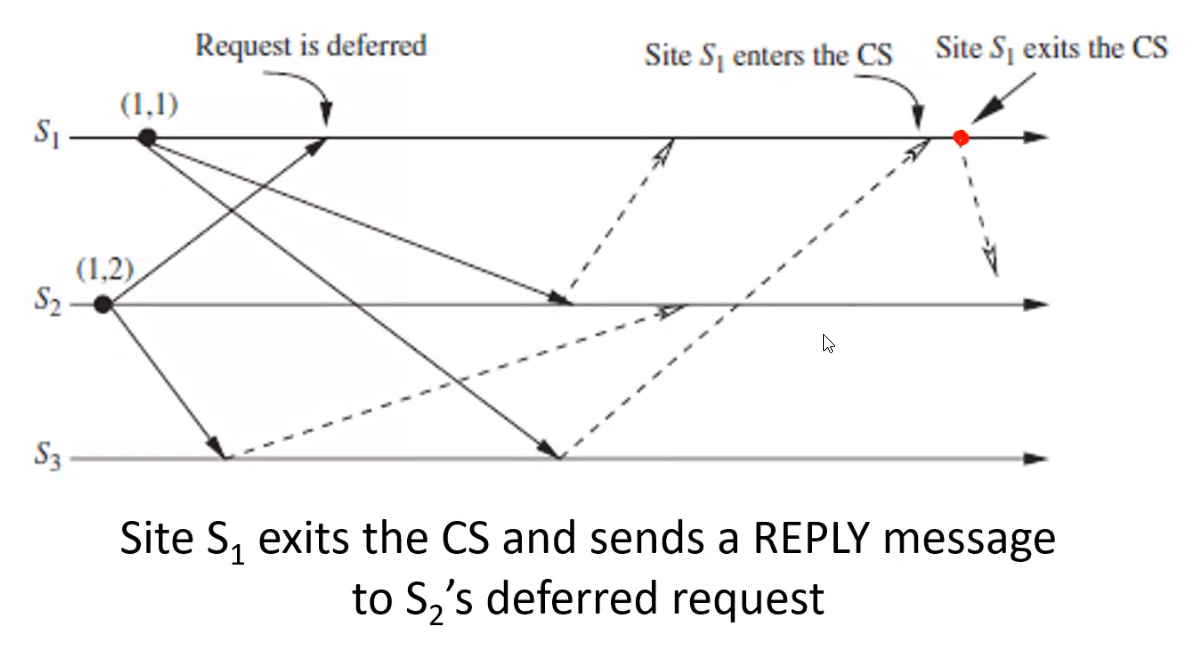
- \(S_1\) finishes executing the CS
- \(S_1\) sends \(REPLY\) to \(S_2\) deferred \(REQUEST\)
- At this point \(RD_1 = [0, 0, 0]\)

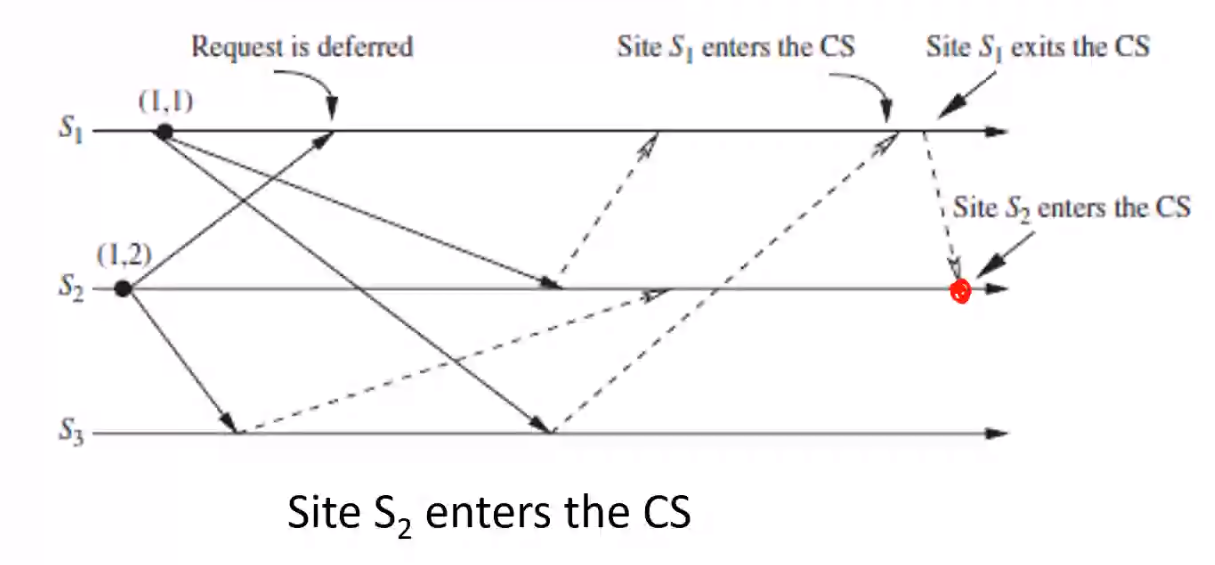
- \(S_2\) enters the CS since \(S_2\) has received \(REPLY\) from all the sites

Performance - requires 2(N - 1) messages per CS execution

Maekawa's Algorithm

• It is a quorum based mutual exclusion algorithm (Explained here Week5DC#Quorum Based)
• Request sets for sites are constructed to satisfy the following conditionsL
  • M1: \(\forall i \forall j, i \ne j, q \le i, j \le N :: R_i \cap R_j \ne \phi\)
  • M2: \(\forall i : 1 \le i \le N :: S_i \in R_i\)
  • M3: \(\forall i : 1 \le i \le N :: |R_i| = K\) for some \(K\)
  • M4: Any site S_j is contained in K number of R_i's, \(1 \le i\) , \(j \le N\)
• Maekawa showed that \(N = K(K - 1) + 1\)
• This relation gives \(|R_j| = K = \sqrt(N)\)
• Uses \(REQUEST\), \(REPLY\) and \(RELEASE\) messages
• Performance -> \(3\sqrt(N)\) messages per CS invocation

Problem Example

If \(N = 7\)
\(K = 3\)
since there are 7 Sites, there will be 7 Request Sets (\(R_1\) to \(R_7\)) each of size \(K = 3\)

Let us take \(R_1 = {S_1, S_3, S_4}\), then:
- The Request Set \(R_2 = {S_2, S_5, S_6}\) is wrong since M1 is not satisfied
- The Request Set \(R3 = {S_3, S_4}\) is wring since M3 is not satisfied

If the following Request sets are taken:
- \(R_1 = {S_1, S_3, S_4}\)
- \(R_2 = {S_1, S_2, S_5}\)
- \(R_3 = {S_1, S_2, S_3}\)
- \(R_4 = {S_1, S_4, S_6}\)
Then, it is wrong since S_1 is in 4 places and according to M4 only K (3) number of occurrences are allowed

Algorithm Steps

From Recorded Lecture

Deadlocks

From Recorded Lecture

Raymond's Tree Based Algorithm

• Uses a spanning tree of the network
• Each node maintains a \(HOLDER\) variable that provides information about the placement of the privilege in relation to the node itself
• A node stores in its \(HOLDER\) variable the identity of a node that it thinks has the privilege or leads to the node having the privilege
• For 2 nodes \(X\) and \(Y\), if \(HOLDER_X = Y\) the undirected edge between \(X\) and \(Y\) can be redrawn as a directed edge from \(X\) to \(Y\)
• Node containing the privilege is also known as the root node

Example

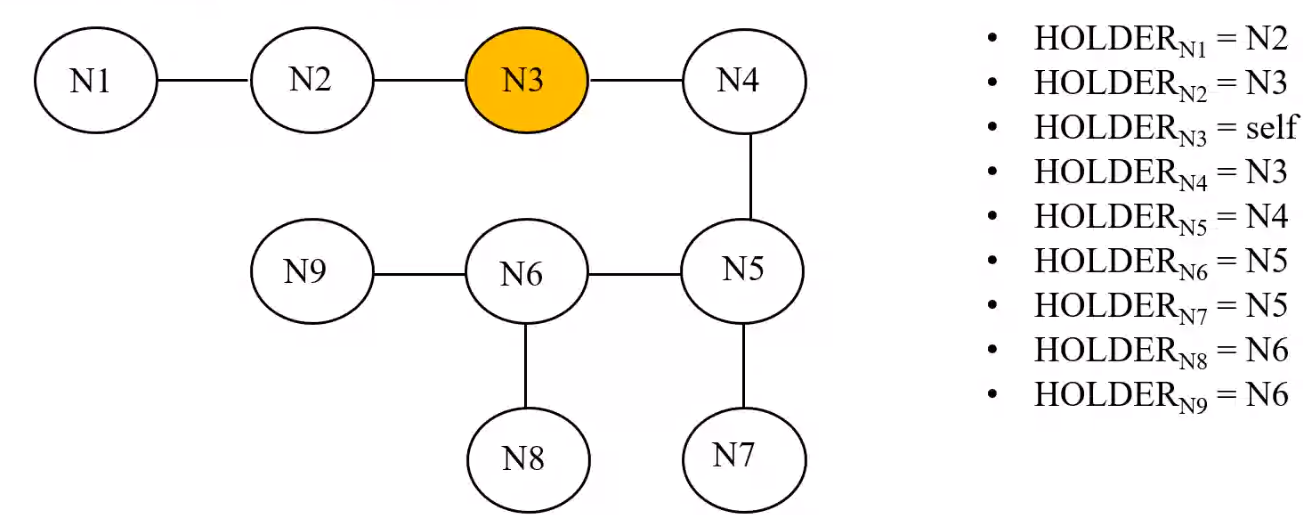
- Messages between nodes traverse along undirected edges of the tree
- Node needs to hold information about and communicate only to its immediate neighboring nodes
- Here \(N3\) holds privilege to itself

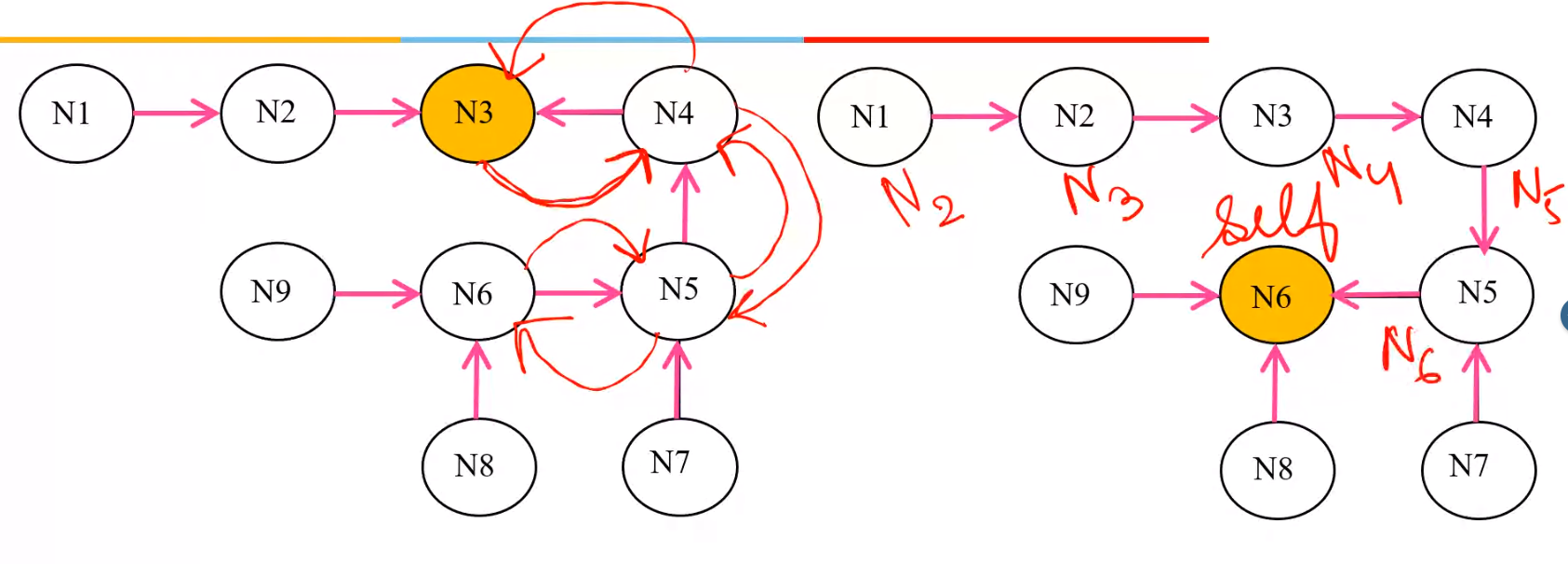
• Consider \(N6\) sends a \(REQUEST\), then it travels along the directed edge
• When \(N3\) receives \(REQUEST\) to give privilege, and it is not using it, then \(N3\) will send message back to whoever sent the \(REQUEST\) and that will further send it down till the node that sent the original \(REQUEST\).
• When that happens the \(HOLDER\) variable for each node changes it when it forwards the \(REQUEST\) back to the original node

Data Structure

• \(HOLDER\)
• \(USING\)
  • Possible values true or false
  • Indicates if the current node is executing the critical section
• \(ASKED\)
  • Possible values true or false
  • Indicates if node has sent a request for the privilege
  • Prevents the sending of duplicate requests for privilege
• \(REQUEST_Q\)
  • FIFO queue that can contain "self" or the identities of immediate neighbors as elements
  • \(REQUEST_Q\) of a node consists of the identities of those immediate neighbors that have requested for privilege but have not yet been sent the privilege
  • Maximum size of \(REQUEST_Q\) of a node is the number of \(immediate neighbors + 1\) (for "self")

Steps of algorithm

From Recorded Lectures

Suzuki-Kasami's Broadcast Algorithm

• Broadcasts a \(REQUEST\) message for the token to all other sites
• Site that possesses the token sends it to the requesting site upon the receipt of its \(REQUEST\) message

• If a site receives a \(REQUEST\) message when it is executing the CS, it sends the token only after it has completed the CS execution

• Distinguish outdated and current REQUEST messages

• \(REQUEST(j, sn)\) where \(sn\) is a sequence number that indicates that \(S_j\) is requesting its \(sn^{th}\) CS execution
• \(S_i\) keeps an array of integers \(RN_i[1, .... , n]\) where \(RN_i[i]\) is the largest sequence number received in a \(REQUEST\) message so far from \(S_j\)
• When \(S_i\) receives a \(REQUEST(j, sn)\) message, it sets \(RN_i[j] = max(RN_i[j], sn)\)
• When \(S_i\) receives a \(REQUEST(j, sn)\) message, the request is outdated if \(RN_i[j] > sn\)

---

Tags: !DistributedComputingIndex