Module 5

Mutual Exclusion

Challenges while using shared resources

1. Simultaneous updates and read to a directory or a file
2. Two processes sending their data to a printer can create chaos to a shared printer

So there is a problem of giving exclusive access to the processes that are asking for these resources

Requirements to be satisfied for such algos

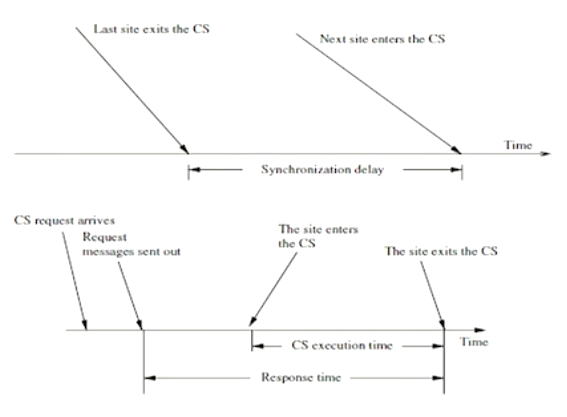
- Performance is measured in terms of
- No. of messages required for CS invocation
- Synchronization delay
- Response time
- System throughput = \(1/(sd + E)\)

A centralized algorithm

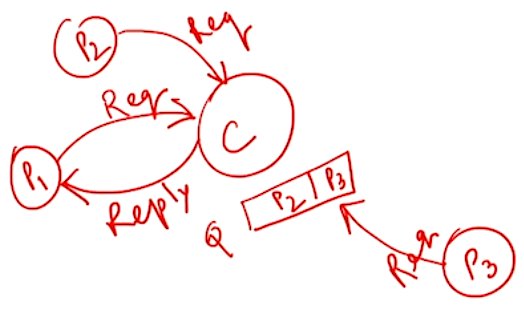
- A central controller \(C\) with a queue \(Q\) for deferring replies
- Request, reply and release messages would have to be sent
- Not reliable since one node is responsible and there are several performance bottlenecks

Lamports Distributed Mutual Exclusion

Requesting the critical section

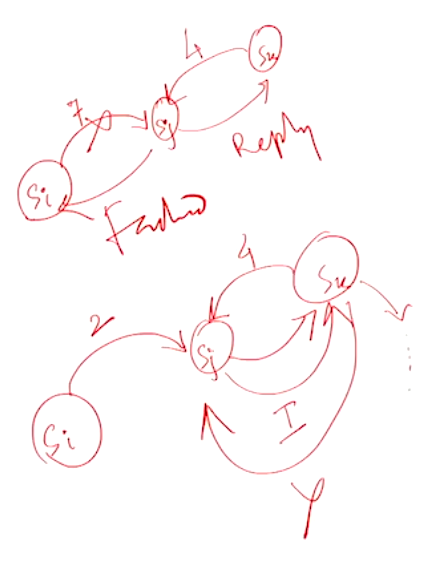
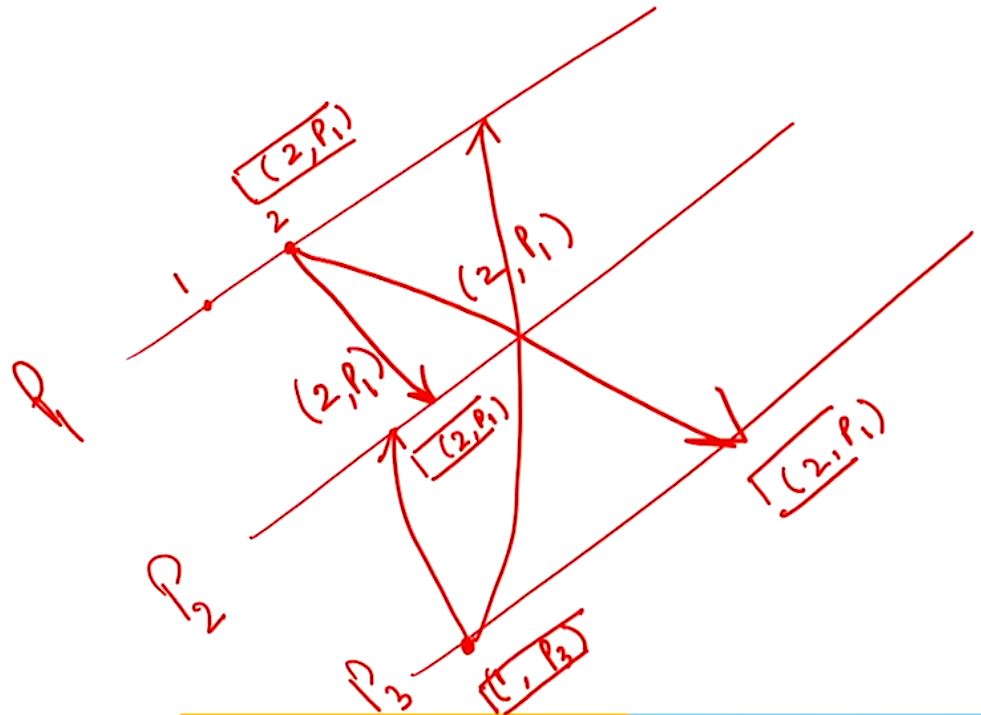
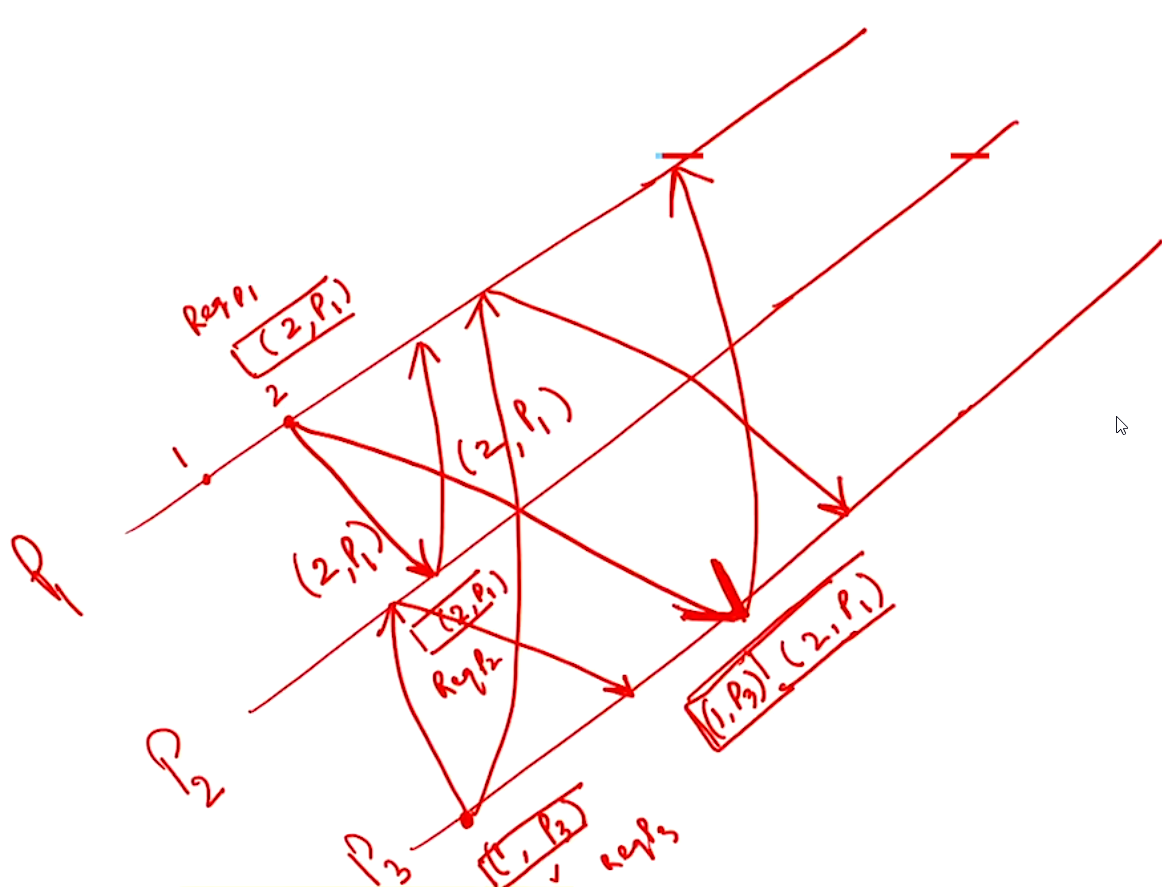
1. When a \(S_i\) wants to enter the \(CS\), it sends a \(REQUEST(T=tsi, i)\) message to all the sites in its request set \(R_i\) and places the request on \(RQ_i\)
2. When a site \(S_j\) receives a \(REQUEST(tsi, i)\) message from the site \(S_i\), it returns a timestamped \(REPLY\) message to \(S_i\) and places site \(S_i\) request on \(RQ_j\)

Executing the CS

Site \(S_i\) enters the CS when the two following conditions hold:
1. \(S_i\) has received a message with timestamp larger than \((tsi, i)\) from all other sites
2. \(S_i\) request is at the top of the \(RQ_i\)

Releasing the CS

1. Site \(S_i\), upon exiting the \(CS\), removes its request from the top of its \(RQ\) and sends a timestamped \(RELEASE\) message to all the sites in its request set \(R_i\)
2. When a site \(S_j\) receives this \(RELEASE\) message, it removes the \(REQUEST\) form \(S_i\) from its \(RQ\)
3. After this, its own process can come to the top of the queue and enter into the \(CS\)

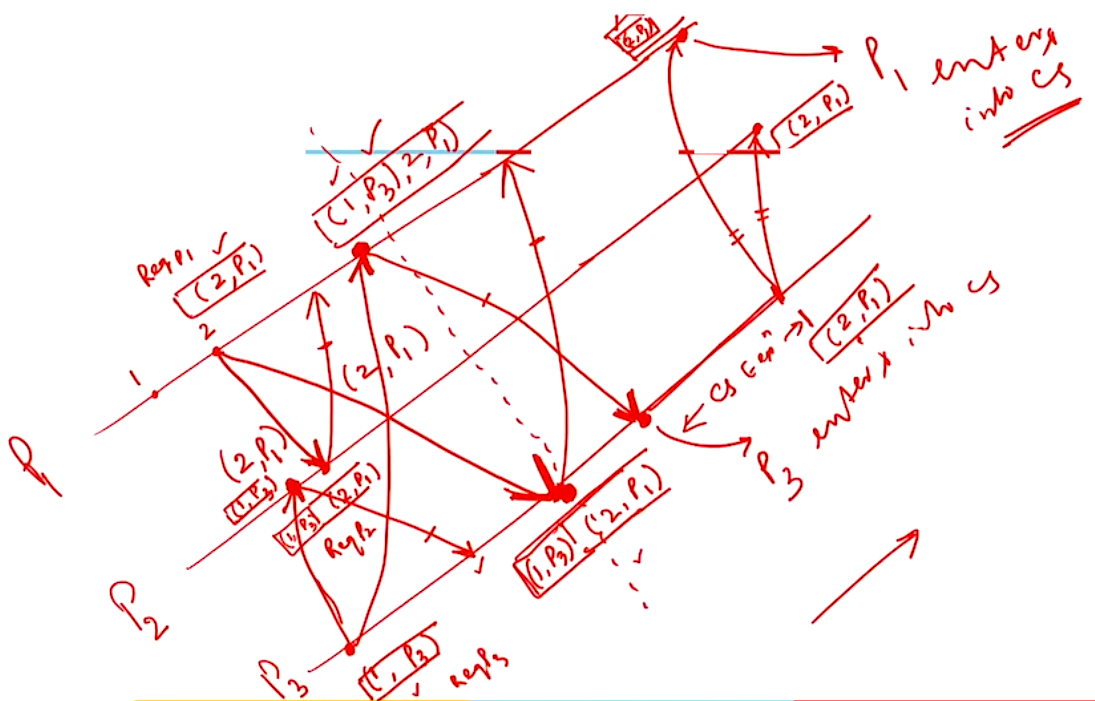
Example

Correctness

• There can never be two different sites \(S_i\) and \(S_j\) being in the \(CS\) since, the \(RQ\) makes sure the order of requests is maintained
• The total Number of messages \(= 3 (N - 1)\)
  • \(REQUEST = N - 1\)
  • \(REPLY = N - 1\)
  • \(RELEASE = N - 1\)

Ricart Agrawala

Requesting Site

A site P_i sends a message REQUEST(ts, i) to all sites

Receiving Site

• Upon receiving the request message, the site \(P_j\) will immediately send a timestamped \(REPLY(ts, j)\) message if and only if :
  • \(P_j\) is not requesting or executing the \(CS\) OR
  • \(P_j\) is requesting the CS buyt sent a request with a higher \(ts\) than the \(ts\) of \(REQUEST\) \(P_i\)
• Else, \(P_j\) will defer the \(REPLY\) to \(P_i\)

Example

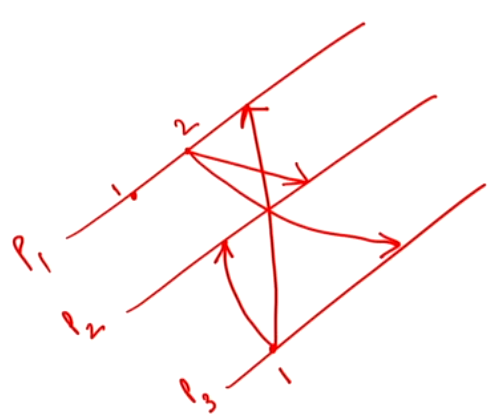
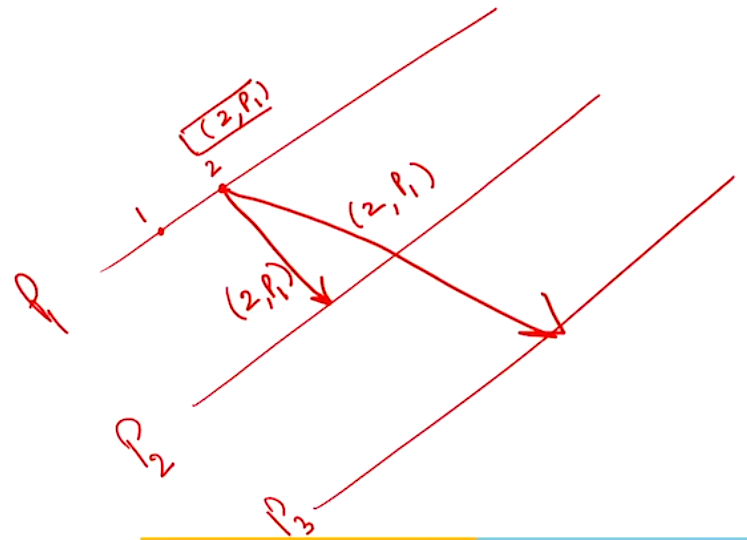
- \(P_2\) sends \(REPLY\) to \(P_3\) and \(P_1\) immediately

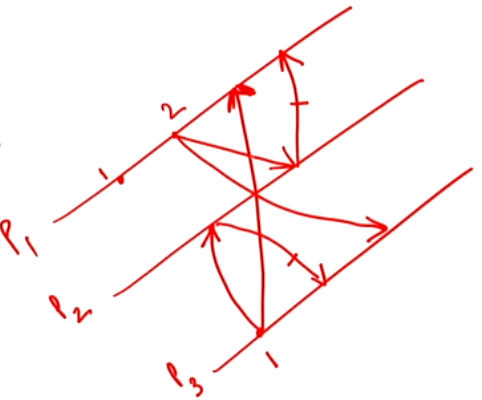
• \(P_1\) sends \(REPLY\) to \(P_3\) since the \(ts\) in the \(REQUEST\) is \(1\) and the \(ts\) for \(P_1\) \(REQUEST\) is \(2\) and \(1 < 2\)
• \(P_3\) defers \(REPLY\) to \(P_1\) since the \(ts\) in the \(REQUEST\) is \(2\) and the \(ts\) for \(P_3\) \(REQUEST\) is \(1\) and \(2 > 1\)

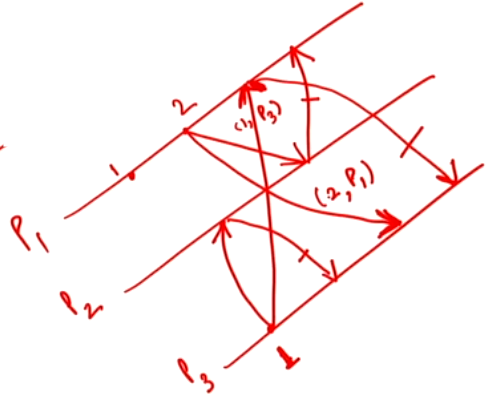
• \(P_3\) enters into \(CS\) since both the replies are received.
• Once \(P_3\) finishes executing it will see the deferred queue to see who to send the reply to.
• After sending reply \(P_1\) goes into \(CS\)

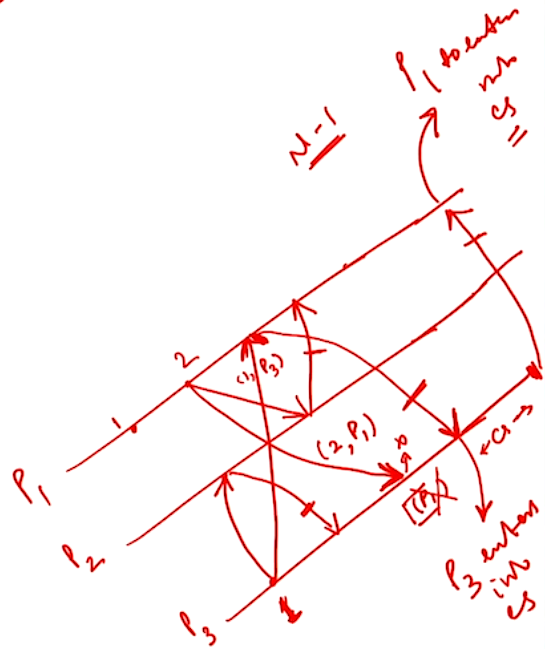
Maekawas Algorithm

Some properties

Request Set rules

Also \(N = K(K - 1) + 1\)

Example Request sets

\(N = 3\)

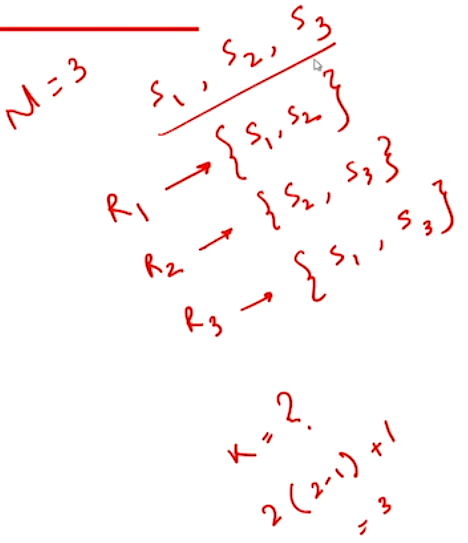
\(N = 7\)

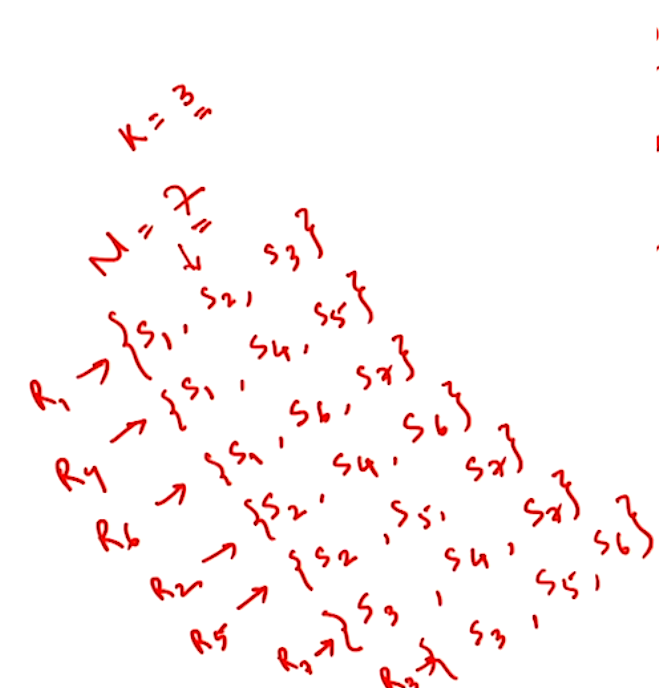
\(N = 13\)

Algorithm

Example

Normal Execution

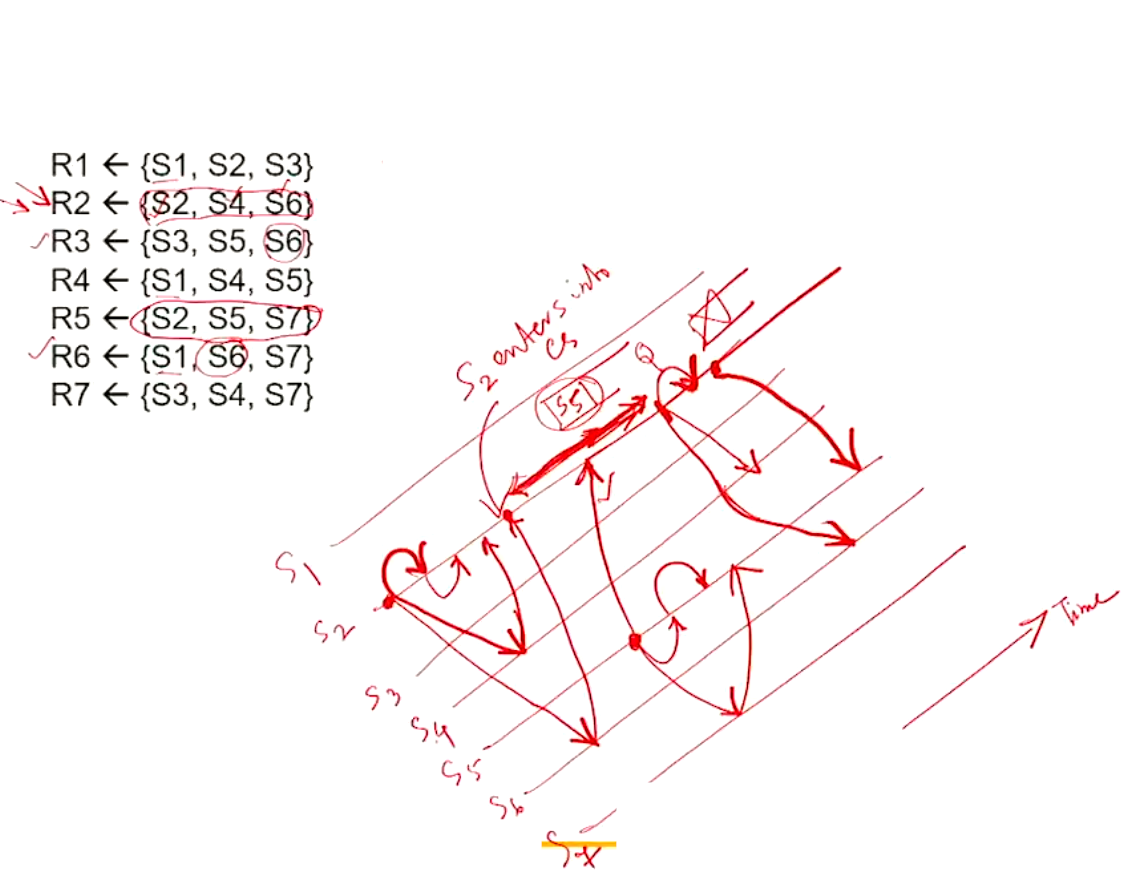
Deadlock Case

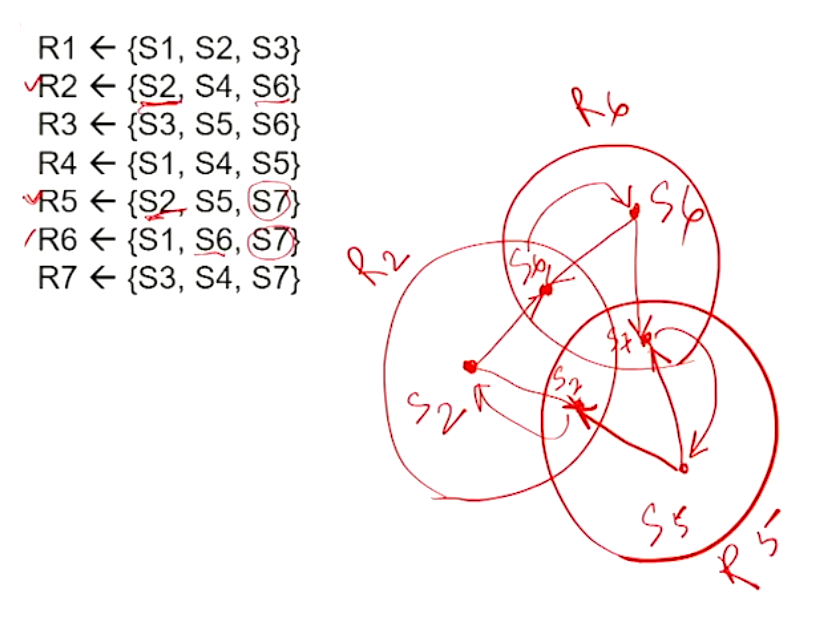
Handling Deadlocks

---

Tags: !DistributedComputingIndex