Week 8#
Lecturer: Pritam Bhattacharya, BITS Pilani, Goa Campus
Date: 18/Sep/2021
Topics Covered#
- Solving Recurrence Relations
- Methods of solving recurrence relations
- Substitution Method
- Recurrence Tree Method
- Masters Theorem
- Methods of solving recurrence relations
Solving Recurrence Relations#
Taking the example of binary search, we can see that the function intially takes in n inputs adn then does constant operations for checking the validity of the iteration and to calculate the mid element. Once this is done the array is divided by two again and the same happens again. This would look like:
\(T(n) = \mathcal{O}(1) + T({n \over 2})\)
\(\implies T(n) = \mathcal{O}(log(n))\)
Methods of solving recurrence relations#
Substitution Method#
We guess a solution, and the check whether it is correct
Example 1: Let us consider for binary search as \(T(n) = \mathcal{O}(log(n))\), which means that we must have \(T(n) \le c.(log(n))\) for large enough \(n\) (for all \(n \ge n_0\))
\(T(n) = \mathcal{O}(1) + T({n \over 2})\)
\(T(n) \le \mathcal{O}(1) + \mathcal{O}(log({n \over 2}))\)
\(T(n) \le c_1 + c_2.log({n \over 2})\)
\(T(n) \le c_1 + c_2.log(n) - c_2.log(2)\)
\(T(n) \le c_1 + c_2.log(n) - c_2\)
\(T(n) \le c_2.log(n) - (c_2 - c_1)\)
\(\implies T(n) \le c_2.log(n)\)
\(\implies T(n) = \mathcal{O}(log(n))\)
Example 2: Let us now consider merge sort. We know that merge sort works by splitting the array into two and then sorting the sub arrays and then merging it back. This would look like this \(T(n) = 2.T({n \over 2}) + \mathcal{O}(n)\)
#### Recurrence Tree Method
This analysis can be seen in the sorting algorithms that were explained earlier.
#### Masters Theorem
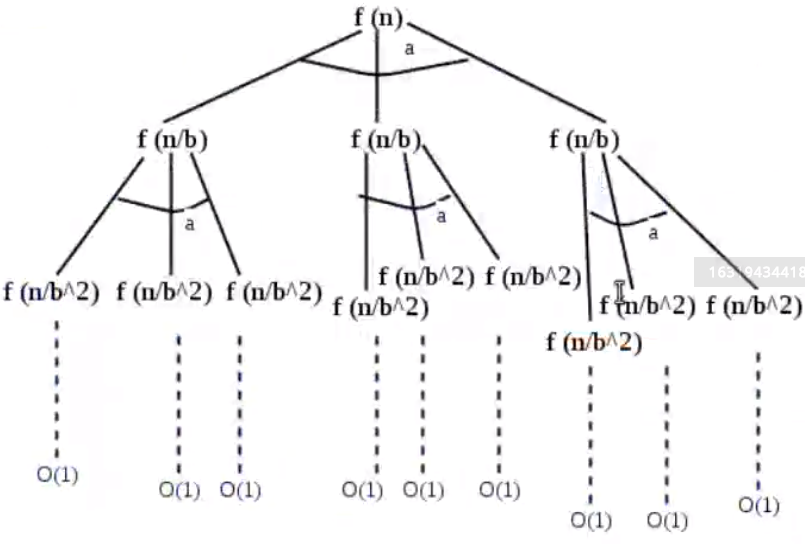
It is a direct method to get solutions for recurrences of the form \(T(n) = a.T(n/b) + \mathcal{O}(n^c)\), and \(a \ge 1\) and \(b \gt 1\) then there are the following three cases to obtain the solutions directly:
- If \(c \lt log_b(a)\), then \(T(n) = \Theta(n^{log_b(a)})\)
- If \(c = log_b(a)\), then \(T(n) = \Theta(n^c.log(n))\)
- If \(c \gt log_b(a)\), then \(T(n) = \Theta(n^c)\)
##### Examples:
Binary Search:
- \(T(n) = T({n \over 2}) + \mathcal{O}(1)\)
- \(a = 1\), \(b = 2\) and \(c = 0\)
- Falls under second case so \(T(n) = \Theta(n^0 log(n)) = \Theta(log(n))\)
